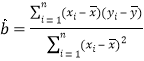题目内容
【题目】已知函数![]() .
.
(1)讨论![]() 在
在![]() 上的零点个数;
上的零点个数;
(2)当![]() 时,若存在
时,若存在![]() ,使
,使![]() ,求实数
,求实数![]() 的取值范围.(
的取值范围.(![]() 为自然对数的底数,其值为2.71828……)
为自然对数的底数,其值为2.71828……)
【答案】(1)见解析;(2)![]()
【解析】
(1)构造函数![]() ,先将讨论
,先将讨论![]() 在
在![]() 上的零点个数问题,转化为讨论直线
上的零点个数问题,转化为讨论直线![]() 与曲线
与曲线![]() 的交点个数问题,用导数方法研究函数
的交点个数问题,用导数方法研究函数![]() 单调性,求出值域,即可得出结果;
单调性,求出值域,即可得出结果;
(2)根据(1)的结果,由![]() 求出零点,得到
求出零点,得到![]() ,再由题意得到
,再由题意得到![]() 成立,构造函数
成立,构造函数![]() ,用导数方法研究其单调性,进而可求出结果.
,用导数方法研究其单调性,进而可求出结果.
(1)由![]() 得
得![]() ,令
,令![]() ,
,
因此讨论![]() 在
在![]() 上的零点个数,即是讨论直线
上的零点个数,即是讨论直线![]() 与曲线
与曲线![]() 的交点个数,
的交点个数,
∵![]() ,
,![]() 在
在![]() 上恒成立,
上恒成立,
故![]() 在
在![]() 上单调递增,
上单调递增,![]() ,
,
又![]() 连续不断,所以当
连续不断,所以当![]() 时,
时,![]() 在
在![]() 上无零点;
上无零点;
当![]() 时,
时,![]() 在
在![]() 上存在一个零点.
上存在一个零点.
(2)当![]() 时,由(1)得
时,由(1)得![]() 在
在![]() 上存在一个零点,
上存在一个零点,
由![]() 得
得![]() ,
,
由(1)可得![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
所以![]() ,
,
又存在![]() ,使
,使![]() 成立,
成立,
所以,只需![]() 成立,即
成立,即![]() 不等式成立,
不等式成立,
令![]() ,
,
则![]() ,
,
易知![]() 在
在![]() 上恒成立,
上恒成立,
故![]() 在
在![]() 上单调递增
上单调递增
又![]() ,所以
,所以![]() .
.
故实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
相关题目
【题目】根据以往的经验,某建筑工程施工期间的降水量![]() (单位:
(单位:![]() )对工期的影响如下表:
)对工期的影响如下表:
降水量 |
|
|
|
|
工期延误天数 | 0 | 1 | 3 | 6 |
根据某气象站的资料,某调查小组抄录了该工程施工地某月前![]() 天的降水量的数据,绘制得到降水量的折线图,如下图所示.
天的降水量的数据,绘制得到降水量的折线图,如下图所示.

(1)求这![]() 天的平均降水量;
天的平均降水量;
(2)根据降水量的折线图,分别估计该工程施工延误天数![]() 的概率.
的概率.
【题目】某商品要了解年广告费![]() (单位:万元)对年利润
(单位:万元)对年利润![]() (单位:万元)的影响,对近4年的年广告费
(单位:万元)的影响,对近4年的年广告费![]() 和年利润
和年利润![]() 数据作了初步整理,得到下面的表格:
数据作了初步整理,得到下面的表格:
广告费 | 2 | 3 | 4 | 5 |
年利润 | 26 | 39 | 49 | 54 |
(Ⅰ)用广告费作解释变量,年利润作预报变量,建立![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(Ⅱ)根据(Ⅰ)的结果预报广告费用为6万元时的年利润.
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: ,
,![]() .
.