题目内容
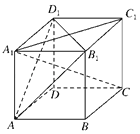
【题目】已知正方体
的棱长为1，给出下列四个命题：①对角线
被平面
和平面
三等分；②正方体的内切球，与各条棱相切的球，外接球的表面积之比为
；（3）以正方体的顶点为顶点的四面体的体积都是
；④正方体与以
为球心，1为半径的球的公共部分的体积是
，其中正确命题的序号为__________.
【答案】①②④.
【解析】
根据点、直线、平面之间的位置关系的定理，以及各种空间几何体的体积计算公式，逐项判断，即可得到本题答案.
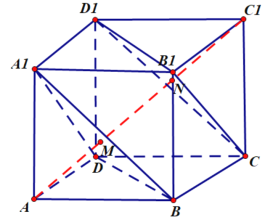
①如图所示，假设对角线
与平面
相交于点M，可得
平面，所以
，解得
，因此对角线被平面和平面
三等分，正确；
②易得正方体的内切球、与各条棱相切的球、外接球的半径分别为
，
因此表面积之比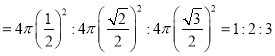
，正确；
③以
为顶点的三棱锥的体积
，不正确；
④正方体与以A为球心，1为半径的球的公共部分的体积
，正确.
故答案为：①②④
同步轻松练习系列答案
课课通课程标准思维方法与能力训练系列答案
【题目】假设关于某设备的使用年限x（年）和所支出的维修费用y万元有如下的统计资料：
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
（1）画出散点图并判断是否线性相关；
（2）如果线性相关，求线性回归方程；
（3）估计使用年限为10年时，维修费用是多少？
附注：①参考公式：回归方程
中斜率和截距的最小二乘估计分别为
；
②参考数据：
【题目】某网购平台为了解某市居民在该平台的消费情况，从该市使用其平台且每周平均消费额超过100元的人员中随机抽取了100名，并绘制如图所示频率分布直方图，已知中间三组的人数可构成等差数列.
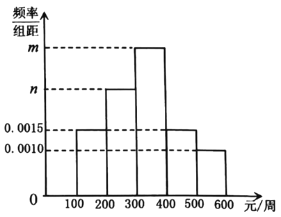
（1）求
的值；
（2）分析人员对100名调查对象的性别进行统计发现，消费金额不低于300元的男性有20人，低于300元的男性有25人，根据统计数据完成下列
列联表，并判断是否有
的把握认为消费金额与性别有关？
（3）分析人员对抽取对象每周的消费金额
与年龄
进一步分析，发现他们线性相关，得到回归方程
.已知100名使用者的平均年龄为38岁，试判断一名年龄为25岁的年轻人每周的平均消费金额为多少.（同一组数据用该区间的中点值代替）
列联表
男性 | 女性 | 合计 | |
消费金额 | |||
消费金额 | |||
合计 |
临界值表：
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
，其中
