Question

7．在平面直角坐标系xOy中，点M是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）上的点，以M为圆心的圆与x轴相切于椭圆的焦点F，圆M与y轴相交于P，Q两点．若△PQM是锐角三角形，则该椭圆离心率的取值范围是（$\frac{\sqrt{6}-\sqrt{2}}{2}$，$\frac{\sqrt{5}-1}{2}$）．

Answer 1

分析 如图所示．把x=c代入椭圆方程可得：$\frac{{c}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$，解得M$（c，\frac{{b}^{2}}{a}）$．过点M作MD⊥y轴，垂足为D．由于△PQM是锐角三角形，可得∠QMD=∠PMD$＜\frac{π}{4}$．因此cos∠QMD=$\frac{|MD|}{|QM|}$=$\frac{c}{\frac{{b}^{2}}{a}}$＞$cos\frac{π}{4}$=$\frac{\sqrt{2}}{2}$，化简整理即可得出．

解答 解：如图所示．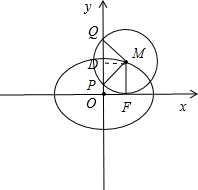
把x=c代入椭圆方程可得：$\frac{{c}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$，解得y=$\frac{{b}^{2}}{a}$．
∴M$（c，\frac{{b}^{2}}{a}）$．
过点M作MD⊥y轴，垂足为D．
∵△PQM是锐角三角形，
∴∠QMD=∠PMD$＜\frac{π}{4}$，$c＜\frac{{b}^{2}}{a}$．
∴cos∠QMD=$\frac{|MD|}{|QM|}$=$\frac{c}{\frac{{b}^{2}}{a}}$＞$cos\frac{π}{4}$=$\frac{\sqrt{2}}{2}$，ac＜a²-c²，
化为$\sqrt{2}ac＞{a}^{2}-{c}^{2}$，ac＜a²-c²
∴${e}^{2}+\sqrt{2}e-1$＞0，e²+e-1＜0．
解得e＞$\frac{\sqrt{6}-\sqrt{2}}{2}$，$e＜\frac{\sqrt{5}-1}{2}$．
∴该椭圆离心率的取值范围是（$\frac{\sqrt{6}-\sqrt{2}}{2}$，$\frac{\sqrt{5}-1}{2}$）．
故答案为：（$\frac{\sqrt{6}-\sqrt{2}}{2}$，$\frac{\sqrt{5}-1}{2}$）．

点评 本题考查了椭圆的标准方程及其性质、圆的性质、锐角三角形的性质、三角函数的单调性，考查了推理能力与计算能力，属于中档题．