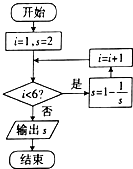
题目内容
16.已F1,F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左右焦点,l为其左准线,其左支上存在一点P使得|PF1|是P到l的距离d与|PF2|的等比中项,求双曲线的离心率的范围.分析 根据双曲线的定义,结合离心率的概念,列出不等式,求出离心率的取值范围.
解答 解:设在左支上存在P点,使|PF1|2=|PF2|•d,
由双曲线的第二定义知$\frac{|{PF}_{1}|}{d}$=$\frac{|{PF}_{2}|}{|{PF}_{1}|}$=e,
即|PF2|=e|PF1|①
再由双曲线的第一定义,得|PF2|-|PF1|=2a.②
由①②,解得|PF1|=$\frac{2a}{e-1}$,|PF2|=$\frac{2ae}{e-1}$,
∵|PF1|+|PF2|≥|F1F2|,
∴$\frac{2a}{e-1}$+$\frac{2ae}{e-1}$≥2c.③
利用e=$\frac{c}{a}$,由③得e2-2e-1≤0,
解得1-$\sqrt{2}$≤e≤1+$\sqrt{2}$;
又e>1,
∴1<e≤1+$\sqrt{2}$;
所以,双曲线离心率的取值范围是(1,1+$\sqrt{2}$].
点评 本题考查了双曲线的定义与几何性质的应用问题,解题时应利用双曲线的第一、第二定义求解,是综合性题目.

练习册系列答案
相关题目
6.在△ABC中,若cos2A+cos2B>2cos2C,则△ABC的形状是( )
| A. | 钝角三角形 | B. | 直角三角形 | C. | 锐角三角形 | D. | 不能确定 |
 如图,在△ABC中,点M是BC的中点,点N在边AC上,且AN=3NC,AM与BN相交于点P,求AM:PM的值.
如图,在△ABC中,点M是BC的中点,点N在边AC上,且AN=3NC,AM与BN相交于点P,求AM:PM的值. 如图所示,四凌锥P-ABCD的底面ABCD为矩形,E.F,H分别AB,CD,PD的中点,求证:平面AFH∥平面PCE.
如图所示,四凌锥P-ABCD的底面ABCD为矩形,E.F,H分别AB,CD,PD的中点,求证:平面AFH∥平面PCE.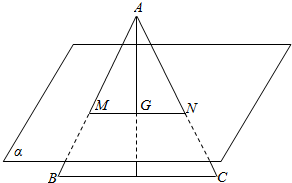 如图,在△ABC中,AB=5,AC=7,∠BAC=90°,G是△ABC的重心,过G的平面α与BC平行,AB∩α=M,AC∩α=N,则MN=$\frac{2}{3}$$\sqrt{74}$.
如图,在△ABC中,AB=5,AC=7,∠BAC=90°,G是△ABC的重心,过G的平面α与BC平行,AB∩α=M,AC∩α=N,则MN=$\frac{2}{3}$$\sqrt{74}$.