题目内容

椭圆
x2
16
+
y2
m
=1过点（2，3），椭圆上一点P到两焦点F1、F2的距离之差为2，
（1）求椭圆方程
（2）试判断△PF1F2的形状．
（1）∵椭圆
x2
16
+
y2
m
=1过点（2，3），
∴
22
16
+
32
m
=1
∴m=12，
∴椭圆方程为：
x2
16
+
y2
12
=1．
（2）：由|PF1|+|PF2|=8，|PF1|-|PF2|=2，解得|PF1|=5，|PF2|=3．
又|F1F2|=4，故满足|PF2|2+|F1F2|2=|PF1|2．
∴△PF1F2为直角三角形．
练习册系列答案
相关题目
如图，直角梯形ABCD中∠DAB=90°，AD∥BC，AB=2，AD=
3
2
，BC=
1
2
．椭圆G以A、B为焦点且经过点D．
（Ⅰ）建立适当坐标系，求椭圆G的方程；
（Ⅱ）若点E满足
EC
=
1
2
AB
，问是否存在不平行AB的直线l与椭圆G交于M、N两点且|ME|=|NE|，若存在，求出直线l与AB夹角正切值的范围，若不存在，说明理由．
若方程
x2
25-m
+
y2
16+m
=1表示焦点在y轴上的椭圆，则实数m的取值范围是（　　）
A．（-16，25）B．(
9
2
，25)		C．(-16，
9
2
)		D．(
9
2
，+∞)
椭圆ax2+by2=1与直线x+y-1=0相交于A，B两点，C是AB的中点，若|AB|=2
2
，OC的斜率为
2
2
，求椭圆的方程．
中心在原点，焦点在y轴，离心率为
1
2
的椭圆方程可能为（　　）
A．
x2
4
+
y2
3
=1		B．
x2
3
+
y2
4
=1		C．
x2
4
+y2=1		D．x2+
y2
4
=1
在焦点在x轴的椭圆过点P（3，0），且长轴长是短轴长的3倍，则其标准方程为______．
分别求适合下列条件的曲线的标准方程：
（1）焦点为F1（0，-1）、F2（0，1）且过点M（
3
2
，1）椭圆；
（2）求经过点A（0，4），B（4，6）且圆心在直线x-2y-2=0上的圆的方程；
（3）与双曲线x2-
y2
2
=1有相同的渐近线，且过点（2，2）的双曲线．
已知点P为椭圆C：
x2
4
+
y2
3
=1上动点，F1，F2分别是椭圆C的焦点，则|PF1|-|PF2|的最大值为（　　）
A．2B．3C．2
3
D．4
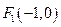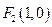若椭圆的两个焦点为，，长轴长为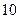，则椭圆的方程为        。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网