题目内容

已知点P为椭圆C：
x2
4
+
y2
3
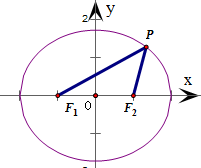
=1上动点，F1，F2分别是椭圆C的焦点，则|PF1|-|PF2|的最大值为（　　）
A．2B．3C．2
3
D．4
∵点P为椭圆C：
x2
4
+
y2
3
=1上动点，
∴a=2，b=
3
，可得c=
a2-b2
=1
运动点P可得|PF1|∈[a-c，a+c]，即|PF1|∈[1，3]
当P与椭圆的左顶点重合时，|PF1|的最小值为1；当P与椭圆的右顶点重合时，
|PF1|的最大值为3
同理，P与椭圆的左顶点重合时，|PF2|的最大值为3；当P与椭圆的右顶点重合时，|PF2|的最小值为1
∴当P与椭圆的右顶点重合时，|PF1|-|PF2|达到最大值，最大值为3-1=2．
故选：A
练习册系列答案
相关题目
椭圆
x2
16
+
y2
m
=1过点（2，3），椭圆上一点P到两焦点F1、F2的距离之差为2，
（1）求椭圆方程
（2）试判断△PF1F2的形状．
点P(2cosα，
3
sinα)（α∈R）与椭圆C：
x2
4
+
y2
3
=1的位置关系是（　　）
A．点P在椭圆C上
B．点P与椭圆C的位置关系不能确定，与α的取值有关
C．点P在椭圆C内
D．点P在椭圆C外
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左右焦点分别为F1，F2，若△AF1F2为正三角形且周长为6；
（1）求椭圆C的标准方程；
（2）若椭圆C上存在A，B两点关于直线y=x+m对称，求实数m的取值范围；
（3）若直线l：y=kx+n与椭圆C交于A，B两点（A，B不是左右顶点），且以AB为直径的圆过椭圆C的右顶点，求证直线l过定点，并求出定点坐标．
已知实数4，m，9构成一个等比数列，则圆锥曲线x2+
y2
m
=1的离心率为（　　）
A．
30
6
B．
7
C．
30
6
或
7
D．
5
6
或7
已知点P在椭圆
x2
49
+
y2
24
=1上，F1、F2是椭圆的焦点，且PF1⊥PF2，求
（1）|PF1|•|PF2|
（2）△PF1F2的面积．
如图，从椭圆
x2
a2
+
y2
b2
=1（a＞b＞o）上一点P向x轴作垂线，垂足恰好为左焦点F1，又点A是椭圆与x轴正半轴的交点，点B是椭圆与y轴正半轴的交点，且AB∥OP，则椭圆的离心率e=______．
椭圆
x2
36
+
y2
20
=1的离心率e是（　　）
A．
5
3
B．
3
2
C．
3
5
5
D．
2
3
曲线
x2
36
+
y2
9
=1与曲线
x2
36-k
+
y2
9-k
=1(k＜9)的（　　）
A．长、短轴相等B．准线相等
C．离心率相等D．焦距相等

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网