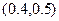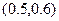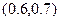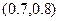题目内容
一位牧民计划用篱笆为他的马群围一个面积为1 600 m2的矩形牧场,由于受自然环境的影响,矩形的一边不能超过a m,求用最少篱笆围成牧场后矩形的长与宽.
当a≥40时,矩形的长与宽都是40 m;
当0<a<40时,矩形的长与宽分别是a m与 m.
m.
当0<a<40时,矩形的长与宽分别是a m与
 m.
m.设一边的长为x m,0<x≤a,则宽为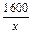 m,矩形的周长为W,
m,矩形的周长为W,
那么W=2(x+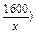 ,则W=2
,则W=2
显然当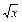 =
=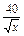 ,即x=40时,
,即x=40时,
若a≥40时,周长W最小,其最小值为160,
此时,矩形的长与宽都是40 m.
若0<a<40时,由于函数W=2(x+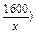 在区间(0,a]上是减函数,则当x=a时,周长W最小,其最小值为2(a+
在区间(0,a]上是减函数,则当x=a时,周长W最小,其最小值为2(a+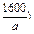 ,此时,矩形的长与宽分别是a m与
,此时,矩形的长与宽分别是a m与 m.
m.
故当a≥40时,矩形的长与宽都是40 m;
当0<a<40时,矩形的长与宽分别是a m与 m.
m.
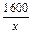 m,矩形的周长为W,
m,矩形的周长为W,那么W=2(x+
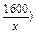 ,则W=2
,则W=2
显然当
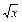 =
=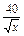 ,即x=40时,
,即x=40时,若a≥40时,周长W最小,其最小值为160,
此时,矩形的长与宽都是40 m.
若0<a<40时,由于函数W=2(x+
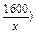 在区间(0,a]上是减函数,则当x=a时,周长W最小,其最小值为2(a+
在区间(0,a]上是减函数,则当x=a时,周长W最小,其最小值为2(a+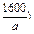 ,此时,矩形的长与宽分别是a m与
,此时,矩形的长与宽分别是a m与 m.
m.故当a≥40时,矩形的长与宽都是40 m;
当0<a<40时,矩形的长与宽分别是a m与
 m.
m.
练习册系列答案
相关题目
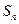 为数列
为数列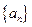 的前
的前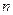 项和,且
项和,且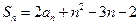 ,
,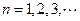 ,(Ⅰ)求证:数列
,(Ⅰ)求证:数列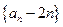 为等比数列;(Ⅱ)设
为等比数列;(Ⅱ)设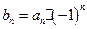 ,求数列
,求数列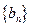 的前
的前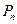 ;(Ⅲ)设
;(Ⅲ)设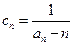 ,数列
,数列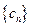 的前
的前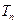 ,求证:
,求证: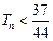 .
.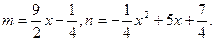

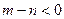
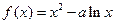 在区间[1,2]上是增函数,且
在区间[1,2]上是增函数,且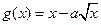 在区间[0,1]上是减函数。
在区间[0,1]上是减函数。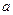 的值;
的值;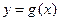 图象上任意一点,求点P到直线
图象上任意一点,求点P到直线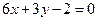 距离的最小值;
距离的最小值; 且
且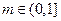 时,
时,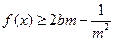 恒成立,求
恒成立,求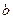 的取值范围。
的取值范围。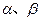 是方程
是方程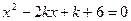 的两个实根,则
的两个实根,则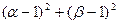 的最小值是多少?
的最小值是多少?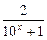 -1(x∈R)的反函数,函数g(x)的图像
-1(x∈R)的反函数,函数g(x)的图像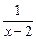 的图像关于y轴对称,设F(x)=f(x)+g(x).
的图像关于y轴对称,设F(x)=f(x)+g(x). 
 ,且
,且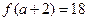 ,
,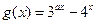 的定义域为[-1,1]。
的定义域为[-1,1]。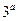 值及函数
值及函数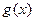 的解析式;
的解析式;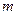 有解,求实数
有解,求实数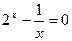 的解所在区间一定是:
的解所在区间一定是: