题目内容
设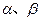 是方程
是方程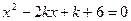 的两个实根,则
的两个实根,则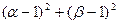 的最小值是多少?
的最小值是多少?
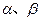 是方程
是方程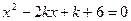 的两个实根,则
的两个实根,则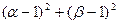 的最小值是多少?
的最小值是多少?当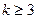 时,
时,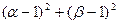 的最小值是8;
的最小值是8;
当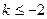 时,
时,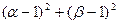 的最小值是18。
的最小值是18。
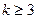 时,
时,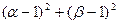 的最小值是8;
的最小值是8;当
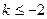 时,
时,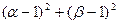 的最小值是18。
的最小值是18。本例只有一个答案正确,设了3个陷阱,很容易上当。
利用一元二次方程根与系数的关系易得: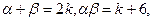
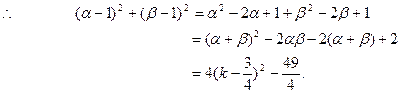
有的学生一看到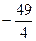 ,常受选择答案(A)的诱惑,盲从附和。这正是思维缺乏反思性的体现。如果能以反思性的态度考察各个选择答案的来源和它们之间的区别,就能从中选出正确答案。
,常受选择答案(A)的诱惑,盲从附和。这正是思维缺乏反思性的体现。如果能以反思性的态度考察各个选择答案的来源和它们之间的区别,就能从中选出正确答案。
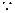 原方程有两个实根
原方程有两个实根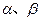 ,∴
,∴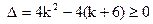 Þ
Þ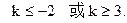
当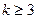 时,
时,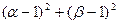 的最小值是8;
的最小值是8;
当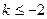 时,
时,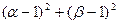 的最小值是18。
的最小值是18。
利用一元二次方程根与系数的关系易得:
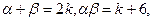
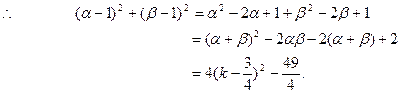
有的学生一看到
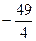 ,常受选择答案(A)的诱惑,盲从附和。这正是思维缺乏反思性的体现。如果能以反思性的态度考察各个选择答案的来源和它们之间的区别,就能从中选出正确答案。
,常受选择答案(A)的诱惑,盲从附和。这正是思维缺乏反思性的体现。如果能以反思性的态度考察各个选择答案的来源和它们之间的区别,就能从中选出正确答案。 原方程有两个实根
原方程有两个实根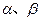 ,∴
,∴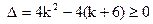 Þ
Þ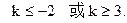
当
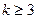 时,
时,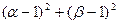 的最小值是8;
的最小值是8;当
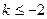 时,
时,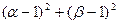 的最小值是18。
的最小值是18。
练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,试写出左边部分的面积y与x的函数解析式,并画出大致图象.
cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,试写出左边部分的面积y与x的函数解析式,并画出大致图象.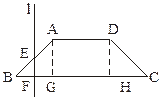
 地10台,
地10台, 地8台.已知从甲地调动1台至
地8台.已知从甲地调动1台至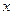 台至
台至 关于台数
关于台数 是该行星绕太阳一周所需的时间.每一行星轨道的半长轴是该行星与太阳之间的最大距离和最小距离的平均值.开普勒发现行星的周期与它的半长轴的
是该行星绕太阳一周所需的时间.每一行星轨道的半长轴是该行星与太阳之间的最大距离和最小距离的平均值.开普勒发现行星的周期与它的半长轴的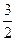 次幂成正比.距离太阳最近的水星,其半长轴为5800万千米,水星的运行周期约为88天.距离太阳最远的冥王星,其半长轴为60亿千米,冥王星的运行周期是多少(以年计)?地球轨道的半长轴为
次幂成正比.距离太阳最近的水星,其半长轴为5800万千米,水星的运行周期约为88天.距离太阳最远的冥王星,其半长轴为60亿千米,冥王星的运行周期是多少(以年计)?地球轨道的半长轴为 亿千米,地球的运行周期是多少(以年计)?
亿千米,地球的运行周期是多少(以年计)?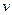 m/s和燃料的质量
m/s和燃料的质量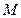 kg,火箭(除燃料外)的质量
kg,火箭(除燃料外)的质量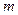 kg的函数关系是
kg的函数关系是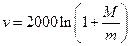 .当燃料质量是火箭质量的多少倍时,火箭的最大速度可达12km/s?
.当燃料质量是火箭质量的多少倍时,火箭的最大速度可达12km/s?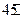 的等腰梯形
的等腰梯形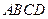 ,底边
,底边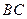 长7 cm,腰长为
长7 cm,腰长为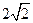 cm,当一条垂直于底边
cm,当一条垂直于底边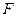 )的直线
)的直线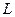 从左至右移动,(与梯形
从左至右移动,(与梯形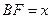 ,试写出左边部分的面积
,试写出左边部分的面积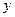 与
与 的函数解析式,并画出大致图象.
的函数解析式,并画出大致图象.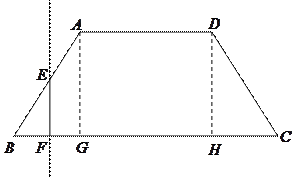
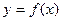
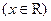 满足
满足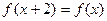 ,且
,且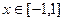 时,
时,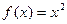 ,则
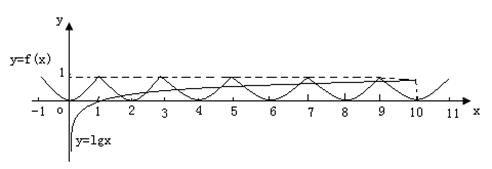
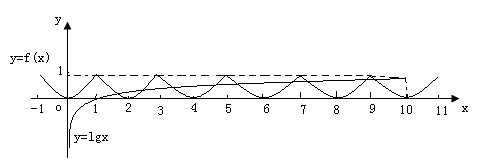
,则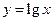 的图象的交点个数为( )
的图象的交点个数为( )
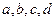 为非负实数,满足
为非负实数,满足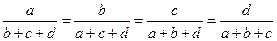 ,则
,则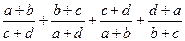 = 。
= 。