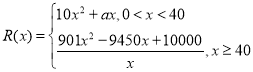题目内容
【题目】已知正四棱锥的底面边长是2,侧棱长是![]() ,则该正四棱锥的全面积为_____.
,则该正四棱锥的全面积为_____.
【答案】12
【解析】
根据正四棱锥的特点,可知侧面是全等的等腰三角形,求出斜高可得侧面积,结合底面积可得全面积.
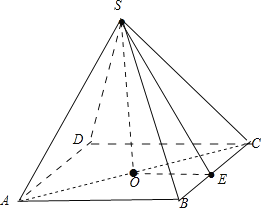
如图在正四棱锥S﹣ABCD中,O为底面正方形的中心,E为BC的中点,连接OE,SO,SE,
则SO⊥平面ABCD,又BC平面ABCD,所以BC⊥SO,
在三角形ABC中,O,E分别为AC,BC的中点,所以OE∥AB,又因为AB⊥BC,所以BC⊥OE.
又OE∩SO=O,所以BC⊥平面SOE,因为SE平面SOE,
所以SE⊥BC,即SE为侧面SBC的斜高,
三角形SBE为直角三角形,所以SE=![]() =2.
=2.
所以该正四棱锥的全面积S全=SABCD+4×SSBC=2×2+4×![]() =4+8=12.
=4+8=12.
故答案为:12.

练习册系列答案
相关题目