题目内容
如图,平行六面体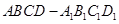 中,侧棱
中,侧棱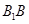 长为3,底面是边长为2的菱形,
长为3,底面是边长为2的菱形,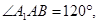
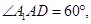 点E在棱
点E在棱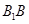 上,则
上,则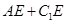 的最小值为( )
的最小值为( )

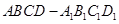 中,侧棱
中,侧棱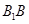 长为3,底面是边长为2的菱形,
长为3,底面是边长为2的菱形,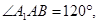
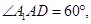 点E在棱
点E在棱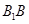 上,则
上,则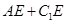 的最小值为( )
的最小值为( )
A.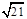 | B.5 | C.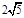 | D.7 |
A
试题分析:

解:将面C1CB1B,B1BAA1打开,如图,由已知得C,B,A共线,连接AC1,则AC1为AE+C1E的最小值,
平行六面体中,侧棱B1B长为3,底面是边长为1的菱形,∠A1AB=120°,∠A1AD=60°,点E在棱B1B上,
∴CA=1+1=2,C1C=3,∴cos∠C1CA=cos60°=
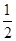 解得C1A=
解得C1A=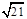 ,故AE+C1E的最小值为
,故AE+C1E的最小值为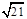 ,故选A.
,故选A.点评:本题考查线段和最小值的求法,解题时要认真审题,仔细解答,注意等价转化思想的合理运用

练习册系列答案
相关题目
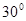 ,则此直线与该平面内任意一条直线所成角的取值范围是 .
,则此直线与该平面内任意一条直线所成角的取值范围是 . 是正方形,
是正方形,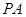 ⊥面
⊥面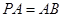 ,
,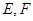 是侧棱
是侧棱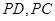 的中点.
的中点.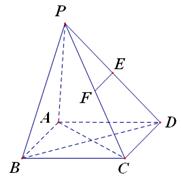
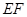 ∥平面
∥平面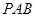 ;
;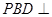 平面
平面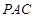 ;
; 与底面
与底面 中,
中, 则
则 所成的角的大小是
所成的角的大小是



 ,且AD⊥BC,对角线BD=
,且AD⊥BC,对角线BD= ,AC=
,AC= , AC和BD所成的角是( )
, AC和BD所成的角是( )



 中,
中, ,
, ,则异面直线
,则异面直线 与
与 所成的角为 ( )
所成的角为 ( )




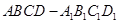 中,
中,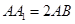 ,E为
,E为 中点,则异面直线BE与
中点,则异面直线BE与 所成角的余弦值为( )
所成角的余弦值为( )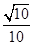
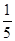
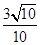

 的侧棱
的侧棱 两两垂直,
两两垂直,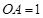 ,
, ,
, 是
是 的中点。
的中点。 与
与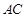 所成角的余弦值;
所成角的余弦值; 的所成角的正弦值。
的所成角的正弦值。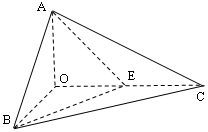
 中,
中, 、
、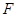 分别为
分别为 和
和 的中点.
的中点.
 和
和 所成的角的余弦值;
所成的角的余弦值; 与平面
与平面 所成的锐二面角的余弦值;
所成的锐二面角的余弦值;