题目内容
在空间四边形ABCD中,已知AD=1,BC= ,且AD⊥BC,对角线BD=
,且AD⊥BC,对角线BD= ,AC=
,AC= , AC和BD所成的角是( )
, AC和BD所成的角是( )
 ,且AD⊥BC,对角线BD=
,且AD⊥BC,对角线BD= ,AC=
,AC= , AC和BD所成的角是( )
, AC和BD所成的角是( )A. | B. | C. | D. |
C
试题分析:
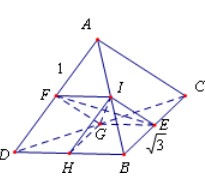
分别取BC、AD、CD、BD、AB中点E、F、G、H、I,
连接EF、EG、EI、FG、FI、GH、GI、HI
∵△BCD中,GE是中位线,∴GE∥BD且GE=
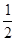 BD
BD 同理可得FI∥BD且FI=
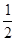 BD
BD∴GE∥FI且GE=FI,得四边形EGFI是平行四边形
∵FG∥AC,GE∥BD
∴∠FGE(或其补角)是异面直线AC和BD所成的角
同理可得∠GHI(或其补角)是异面直线AD和BC所成的角
∵AD⊥BC,∴∠GHI=90°
∵GH=
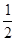 BC=
BC=  ,HI=
,HI=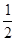 AD=
AD=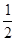 ,∴GI=" GH2+HI2" =1
,∴GI=" GH2+HI2" =1∵平行四边形EGFI中,FI=GE=
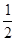 BD=
BD= 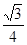 ,FG=EI=
,FG=EI=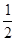 AC=
AC=
∴
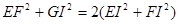 ,得
,得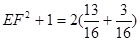 ,解得EF=1
,解得EF=1因此,
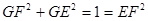 ,可得∠FGE=
,可得∠FGE=
∴异面直线AC和BD所成的角为

点评:本题在空间四边形ABCD中,已知相对棱的长度和所成角,并且知道对角线长度的情况下求对角线
所成角大小,着重考查了空间四边形的性质和异面直线所成角求法等知识,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
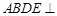 平面
平面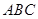 ,
,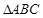 是等腰直角三角形,
是等腰直角三角形,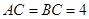 ,四边形
,四边形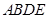 是直角梯形,
是直角梯形,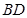 ∥AE,
∥AE,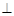
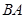 ,
,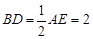 ,
,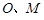 分别为
分别为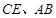 的中点.
的中点.
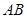 与
与 所成角的大小;
所成角的大小;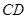 和平面
和平面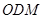 所成角的正弦值.
所成角的正弦值.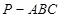 中,
中,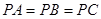 ,底面
,底面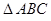 是正三角形,
是正三角形,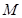 、
、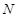 分别是侧棱
分别是侧棱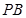 、
、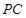 的中点. 若平面
的中点. 若平面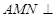 平面
平面 ,则侧棱
,则侧棱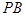 与平面
与平面 所成角的正切值是( )
所成角的正切值是( )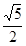
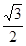
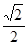
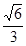
 中,各侧面均为正方形,侧面
中,各侧面均为正方形,侧面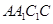 的对角线相交于点
的对角线相交于点 ,则
,则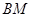 与平面
与平面
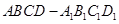 中,侧棱
中,侧棱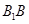 长为3,底面是边长为2的菱形,
长为3,底面是边长为2的菱形,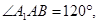
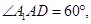 点E在棱
点E在棱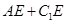 的最小值为( )
的最小值为( )
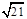
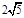
 中,
中,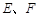 分别为
分别为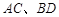 的中点,若
的中点,若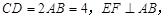 则
则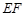 与
与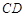 所成的角为
所成的角为



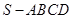 的侧棱长为
的侧棱长为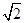 ,底面边长为
,底面边长为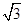 ,
,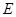 为
为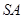 中点,则异面直线
中点,则异面直线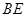 与
与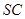 所成的角是 .
所成的角是 .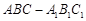 中已知
中已知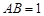 ,
,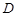 在棱
在棱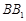 上,且
上,且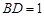 ,若
,若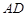 与平面
与平面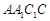 所成的角为
所成的角为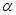 ,则
,则