题目内容
(本题满分16分)
如图,在棱长为1的正方体 中,
中, 、
、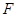 分别为
分别为 和
和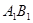 的中点.
的中点.

(1)求异面直线 和
和 所成的角的余弦值;
所成的角的余弦值;
(2)求平面 与平面
与平面 所成的锐二面角的余弦值;
所成的锐二面角的余弦值;
如图,在棱长为1的正方体
 中,
中, 、
、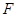 分别为
分别为 和
和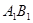 的中点.
的中点.
(1)求异面直线
 和
和 所成的角的余弦值;
所成的角的余弦值;(2)求平面
 与平面
与平面 所成的锐二面角的余弦值;
所成的锐二面角的余弦值;(1)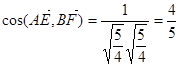 ; (2)
; (2)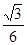 。
。
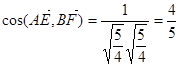 ; (2)
; (2)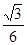 。
。正方体易建立空间直角坐标系,写出点的坐标.(1)求出向量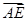 ,
,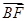 ,把异面直线
,把异面直线 和
和 所成的角的余弦值转化为向量
所成的角的余弦值转化为向量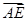 ,
,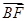 夹角的余弦值的绝对值;(2)求出平面BDD1的与平面BFC1的一个法向量,把平面
夹角的余弦值的绝对值;(2)求出平面BDD1的与平面BFC1的一个法向量,把平面 与平面
与平面 所成的锐二面角的余弦值转化为两法向量的夹角的余弦值的绝对值.
所成的锐二面角的余弦值转化为两法向量的夹角的余弦值的绝对值.
(1)以D为坐标原点,以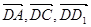 为正交基底建立空间直角坐标系
为正交基底建立空间直角坐标系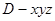 如图,则
如图,则
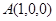 ,
,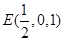 ,
,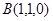 ,
,
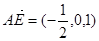 ,
,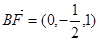
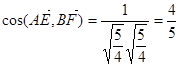 ……………………………………6分
……………………………………6分
异面直线 和
和 所成的角的余弦值;……………………………………7分
所成的角的余弦值;……………………………………7分
(2)平面BDD1的一个法向量为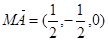
设平面BFC1的法向量为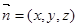
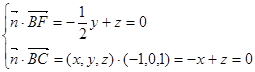 ∴
∴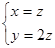
取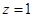 得平面BFC1的一个法向量
得平面BFC1的一个法向量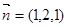
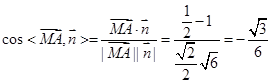 , ……………………………………14分∴所求的余弦值为
, ……………………………………14分∴所求的余弦值为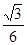 ……………………………………16分
……………………………………16分
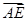 ,
,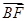 ,把异面直线
,把异面直线 和
和 所成的角的余弦值转化为向量
所成的角的余弦值转化为向量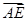 ,
,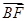 夹角的余弦值的绝对值;(2)求出平面BDD1的与平面BFC1的一个法向量,把平面
夹角的余弦值的绝对值;(2)求出平面BDD1的与平面BFC1的一个法向量,把平面 与平面
与平面 所成的锐二面角的余弦值转化为两法向量的夹角的余弦值的绝对值.
所成的锐二面角的余弦值转化为两法向量的夹角的余弦值的绝对值.(1)以D为坐标原点,以
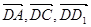 为正交基底建立空间直角坐标系
为正交基底建立空间直角坐标系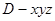 如图,则
如图,则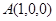 ,
,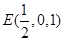 ,
,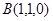 ,
,
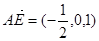 ,
,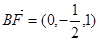
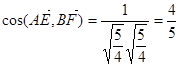 ……………………………………6分
……………………………………6分异面直线
 和
和 所成的角的余弦值;……………………………………7分
所成的角的余弦值;……………………………………7分(2)平面BDD1的一个法向量为
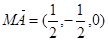
设平面BFC1的法向量为
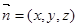
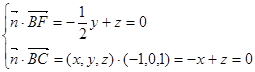 ∴
∴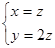
取
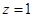 得平面BFC1的一个法向量
得平面BFC1的一个法向量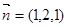
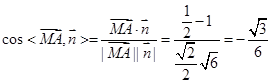 , ……………………………………14分∴所求的余弦值为
, ……………………………………14分∴所求的余弦值为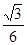 ……………………………………16分
……………………………………16分
练习册系列答案
相关题目
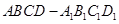 中,侧棱
中,侧棱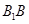 长为3,底面是边长为2的菱形,
长为3,底面是边长为2的菱形,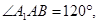
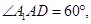 点E在棱
点E在棱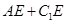 的最小值为( )
的最小值为( )
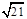
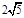
 的正方形
的正方形 沿对角线
沿对角线 成直二面角(平面
成直二面角(平面 平面
平面 ),则
),则 的度数是( )
的度数是( ) B.
B.  C.
C.  D
D 
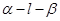 中,
中, 且
且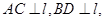 已知
已知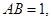
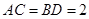 ,
, 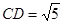 , 则二面角
, 则二面角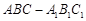 中已知
中已知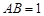 ,
,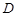 在棱
在棱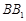 上,且
上,且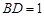 ,若
,若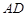 与平面
与平面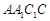 所成的角为
所成的角为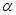 ,则
,则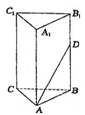




 各棱长均为1,
各棱长均为1, 分别在棱
分别在棱 上,且
上,且 ,则直线
,则直线 与直线
与直线 所成角的正切值的取值范围是
所成角的正切值的取值范围是 
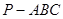 中,
中,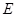 为
为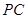 的中点,则
的中点,则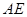 与平面
与平面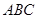 所成的角的正弦值为( )
所成的角的正弦值为( )



 的等腰直角三角形
的等腰直角三角形 与正三角形
与正三角形 所在平面互相垂直,
所在平面互相垂直, 是线段
是线段 的中点,则
的中点,则 与
与 所成角的大小为 .
所成角的大小为 .