题目内容
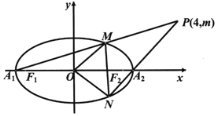
【题目】如图,已知椭圆C:![]() 的左、右项点分别为A1,A2,左右焦点分别为F1,F2,离心率为
的左、右项点分别为A1,A2,左右焦点分别为F1,F2,离心率为![]() ,|F1F2|=
,|F1F2|=![]() ,O为坐标原点.
,O为坐标原点.
(1)求椭圆C的方程;
(2)设过点P(4,m)的直线PA1,PA2与椭圆分别交于点M,N,其中m>0,求![]() 的面积S的最大值.
的面积S的最大值.
【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】
(1)由离心率为![]() ,|F1F2|=2
,|F1F2|=2![]() ,列式计算a,b,即可得椭圆C的方程.
,列式计算a,b,即可得椭圆C的方程.
(2)将直线PA1,PA1的方程:y![]() ,y
,y![]() 分别与椭圆方程联立,得到M、N的坐标,可得直线MN过定点(1,0),故设MN的方程为:x=ty+1,由
分别与椭圆方程联立,得到M、N的坐标,可得直线MN过定点(1,0),故设MN的方程为:x=ty+1,由![]() 结合韦达定理,可得△OMN的面积S
结合韦达定理,可得△OMN的面积S![]() 2
2![]() ,再利用函数单调性即可求出面积最大值.
,再利用函数单调性即可求出面积最大值.
(1)∵离心率为![]() ,
,![]() ,
,
∴ ,∴
,∴![]() ,
,![]() ,则b=1
,则b=1
∴椭圆C的方程的方程为:![]()
(2)由(1)得A1(-2,0),A2(2,0),
直线PA1,PA1的方程分别为:![]() ,
,![]()
由 ,得
,得![]()
∴![]() ,可得
,可得![]() ,
,![]()
由 ,可得
,可得![]()
∴![]() ,可得
,可得![]() ,
,![]()
![]() ,
,
直线MN的方程为:![]() ,
,
![]()
![]()
![]()
可得直线MN过定点(1,0),故设MN的方程为:![]()
由 得
得![]()
设![]() ,
,![]() ,则
,则![]() ,
,![]()
∴![]() ,
,
∴![]() 的面积
的面积![]()
令![]() ,则
,则![]()
∵![]() ,且函数
,且函数![]() 在
在![]() 递增,
递增,
∴当![]() ,S取得最大值
,S取得最大值![]() .
.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
【题目】已知具有线性相关关系的两个变量![]() 之间的几组数据如下表所示:
之间的几组数据如下表所示:
| 2 | 4 | 6 | 8 | 10 |
| 3 | 6 | 7 | 10 | 12 |
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并估计当
,并估计当![]() 时,
时, ![]() 的值;
的值;
(2)将表格中的数据看作五个点的坐标,则从这五个点中随机抽取2个点,求恰有1个点落在直线![]() 右下方的概率.
右下方的概率.
参考公式: 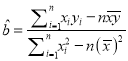 ,
, ![]() .
.