题目内容
【题目】已知线段AB的端点B的坐标为(3,0),端点A在圆![]() 上运动;
上运动;
(1)求线段AB中点M的轨迹方程;
(2)过点C(1,1)的直线m与M的轨迹交于G、H两点,当△GOH(O为坐标原点)的面积最大时,求直线m的方程并求出△GOH面积的最大值.
(3)若点C(1,1),且P在M轨迹上运动,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)设出A,M坐标,利用M为线段AB中点,确定A,M坐标之间的关系,根据点A在圆![]() 上运动,可得线段AB中点M的轨迹方程;(2)令
上运动,可得线段AB中点M的轨迹方程;(2)令![]() ,则
,则![]() ,即
,即![]() 时
时![]() 面积最大为2,从而得到直线m的方程;(3)设点
面积最大为2,从而得到直线m的方程;(3)设点![]() ,则
,则![]() ,令
,令![]() ,由直线与圆的位置关系得到
,由直线与圆的位置关系得到![]() 的取值范围.
的取值范围.
(1)解:设点![]()
由中点坐标公式有
又点![]() 在圆
在圆![]() 上,将
上,将![]() 点坐标代入圆方程得:
点坐标代入圆方程得:
![]() 点的轨迹方程为:
点的轨迹方程为:![]()
(2)令![]() ,则
,则![]()
当![]() ,即
,即![]() 时
时![]() 面积最大为2
面积最大为2
又直线![]() 过点
过点![]() ,
,![]() ,∴
,∴![]() 到直线
到直线![]() 的距离为
的距离为![]() ,当直线
,当直线![]() 斜率不存在时
斜率不存在时![]() ,
,![]() 到
到![]() 的距离为1不满足,令
的距离为1不满足,令![]()
故直线![]() 的方程为:
的方程为:![]()
(3)设点![]() ,由于点
,由于点![]()
则![]() ,令
,令![]()
有![]() ,由于点
,由于点![]() 在圆
在圆![]() 上运动,故满足圆的方程.
上运动,故满足圆的方程.
当直线![]() 与圆相切时,
与圆相切时,![]() 取得最大或最小
取得最大或最小
故有![]()
所以![]()

【题目】在对人们的休闲方式的一次调查中,用简单随机抽样方法调查了125人,其中女性70人,男性55人.女性中有40人主要的休闲方式是看电视,另外30人主要的休闲方式是运动;男性中有20人主要的休闲方式是看电视,另外35人主要的休闲方式是运动.
(1)根据以上数据建立一个![]() 列联表;
列联表;
(2)能否在犯错误的概率不超过0.025的前提下,认为性别与休闲方式有关系?
(3)在休闲方式为看电视的人中按分层抽样方法抽取6人参加某机构组织的健康讲座,讲座结束后再从这6人中抽取2人作反馈交流,求参加交流的恰好为2位女性的概率.
附:
P( | 0.05 | 0.025 | 0.010 |
k | 3.841 | 5.024 | 6.635 |
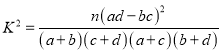
休闲方式 性别 | 看电视 | 运动 | 合计 |
女 | |||
男 | |||
合计 |
【题目】在某区“创文明城区”(简称“创城”)活动中,教委对本区![]() 四所高中学校按各校人数分层抽样,随机抽查了100人,将调查情况进行整理后制成下表:
四所高中学校按各校人数分层抽样,随机抽查了100人,将调查情况进行整理后制成下表:
学校 |
|
|
|
|
抽查人数 | 50 | 15 | 10 | 25 |
“创城”活动中参与的人数 | 40 | 10 | 9 | 15 |
(注:参与率是指:一所学校“创城”活动中参与的人数与被抽查人数的比值)假设每名高中学生是否参与”创城”活动是相互独立的.
(1)若该区共2000名高中学生,估计![]() 学校参与“创城”活动的人数;
学校参与“创城”活动的人数;
(2)在随机抽查的100名高中学生中,随机抽取1名学生,求恰好该生没有参与“创城”活动的概率;
(3)在上表中从![]() 两校没有参与“创城”活动的同学中随机抽取2人,求恰好
两校没有参与“创城”活动的同学中随机抽取2人,求恰好![]() 两校各有1人没有参与“创城”活动的概率是多少?
两校各有1人没有参与“创城”活动的概率是多少?