题目内容
【题目】已知一个动点![]() 到点
到点![]() 的距离比到直线
的距离比到直线![]() 的距离多1.
的距离多1.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,且线段
两点,且线段![]() 中点是点
中点是点![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1) ![]() (2)
(2) ![]()
【解析】
(1)由题意,转化为动点![]() 满足到点
满足到点![]() 的距离比到直线
的距离比到直线![]() 的距离相等,根据抛物线的定义,即可求解抛物线的方程;
的距离相等,根据抛物线的定义,即可求解抛物线的方程;
(2)当直线斜率存在时,设![]() ,代入作差,即可求得直线斜率
,代入作差,即可求得直线斜率![]() ,进而利用正弦的点斜式方程,即可得到结论.
,进而利用正弦的点斜式方程,即可得到结论.
(1)∵动点![]() 满足到点
满足到点![]() 的距离比到直线
的距离比到直线![]() 距离多1,
距离多1,
∴动点![]() 满足到点
满足到点![]() 的距离比到直线
的距离比到直线![]() 的距离相等,
的距离相等,
∴动点![]() 是以
是以![]() 为焦点,
为焦点,![]() 为准线的抛物线,方程为
为准线的抛物线,方程为![]()
(2)当直线斜率不存在时,![]() 显然不为中点,
显然不为中点,
当直线斜率存在时,设为直线斜率![]() ,设
,设![]() ,
,
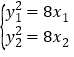 ,得
,得![]() ,
,
∴![]()
又![]() 是线段
是线段![]() 的中点,∴
的中点,∴![]() ,∴
,∴![]()
故直线的方程为![]() ,化为一般形式即:
,化为一般形式即:![]()

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
