题目内容

4．函数f（x）=|log2x|-x+1的零点个数为（　　）
A．1B．2C．3D．4

分析 函数的零点，转化为两个函数的交点个数，得到结果即可．

解答 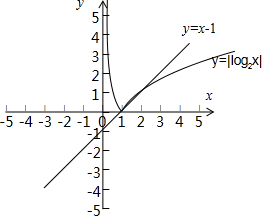解：函数f（x）=|log2x|-x+1的零点个数，就是方程|log2x|-x+1=0的根的个数．也就是函数y=|log2x|与y=x-1交点个数，
如图：可知两个函数的图象交点个数为：2．
故选：B．

点评 本题考查函数的零点与方程的根，数形结合的解题方法，考查计算能力．

练习册系列答案
相关题目
4．若复数z1=$\frac{6+2i}{1-i}$与z2=a+bi（a，b∈R）互为共轭复数，则（　　）
A．a=2，b=-4B．a=2，b=4C．a=-2，b=-4D．a=-2，b=4
5．若$\overrightarrow{a}$=（4，3），$\overrightarrow{b}$=（-1，2），且（$\overrightarrow{a}$-λ$\overrightarrow{b}$）⊥（2$\overrightarrow{a}$+$\overrightarrow{b}$），则λ=$\frac{52}{9}$时，$\overrightarrow{a}$，$\overrightarrow{b}$均为向量．
12．已知函数f（x）对一切实数a、b满足f（a+b）=f（a）•f（b），f（1）=2，（且f（x）恒非零），数列{an}的通项an=$\frac{{{f^2}（n）+f（2n）}}{f（2n-1）}$（n∈N+），则数列{an}的前n项和=4n．
19．已知在△ABC中，a2+c2-b2=ac，log4sinA+log4sinC=-1，△ABC的面积为$\sqrt{3}$
（1）求∠B及b的长度；
（2）求a的长．
9．${∫}_{2}^{t}$（x-2）4dx的展开式中t2的系数是-16．
16．某产品生产厂家根据历年销售经验得到写来关于生活销售的统计规律，每生产产品x（百台）．其总成本为G（x）（万元），其中固定成本为2万元，并且每生产1百台的生产成本为1万元（总成本=固定成本+生产成本），销售收入k（x）（万元）满足：R（x）=$\left\{\begin{array}{l}-0.4{x^2}+4.2x-0.8\;\;\;（0≤x≤5）\\ 10.2\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;（x＞5）.\end{array}\right.$假定该产品产销平衡，求：
（1）生产x百台产品的总利润y（万元）；
（2）工厂生产多少台产品时，可使盈利最高．
13．若x∈[-2，2]，不等式x2+ax+3≥0恒成立，求实数a的取值范围．
14．已知A（-3，4），B（3，2），过点P（1，0）的直线l与线段AB有公共点．
（1）求l的倾斜角α的取值范围；
（2）求l的斜率k的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网