题目内容
4.若复数z1=$\frac{6+2i}{1-i}$与z2=a+bi(a,b∈R)互为共轭复数,则( )| A. | a=2,b=-4 | B. | a=2,b=4 | C. | a=-2,b=-4 | D. | a=-2,b=4 |
分析 利用复数的运算法则、共轭复数的定义即可得出.
解答 解:复数z1=$\frac{6+2i}{1-i}$=$\frac{(6+2i)(1+i)}{(1-i)(1+i)}$=(3+i)(1+i)=2+4i,
∵复数z1=$\frac{6+2i}{1-i}$与z2=a+bi(a,b∈R)互为共轭复数,
∴a=2,b=-4.
故选:A.
点评 本题考查了复数的运算法则、共轭复数的定义,属于基础题.

练习册系列答案
相关题目
14.过点(3,-1),圆心在y轴上,且与x轴相切的圆的方程为( )
| A. | x2+y2-10y=0 | B. | x2+y2+10y=0 | C. | x2+y2+10x=0 | D. | x2+y2-10x=0 |
12.两个三口之家,共4个大人,2个小孩,约定星期日乘“奥迪”、“捷达”两辆轿车结伴郊游,每辆车最多只能乘坐4人,其中两个小孩不能独坐一辆车,则不同的乘车方法种数是( )
| A. | 40 | B. | 48 | C. | 60 | D. | 68 |
9.若直线(m+l)x+(n+l)y-2=0(m,n∈R)与圆(x-l)2+(y-1)2=1相切,则m+n的取值范围是( )
| A. | $[1-\sqrt{3},1+\sqrt{3}]$ | B. | $(-∞,1-\sqrt{3}]∪[1+\sqrt{3},+∞)$ | C. | $[2-2\sqrt{2},2+2\sqrt{2}]$ | D. | $(-∞,2-2\sqrt{2}]∪[2+2\sqrt{2},+∞)$ |
16.下列命题正确的是( )
(1)已知命题p:?x∈R,2x=1.则?p是:?x∈R,2x≠1
(2)设l,m表示不同的直线,α表示平面,若m∥l,且m∥α,则l∥α;
(3)利用计算机产生0~1之间的均匀随机数a,则事件“3a-1>0”发生的概率为$\frac{2}{3}$
(4)“a>0,b>0”是“$\frac{a}{b}+\frac{b}{a}≥2$”的充分不必要条件.
(1)已知命题p:?x∈R,2x=1.则?p是:?x∈R,2x≠1
(2)设l,m表示不同的直线,α表示平面,若m∥l,且m∥α,则l∥α;
(3)利用计算机产生0~1之间的均匀随机数a,则事件“3a-1>0”发生的概率为$\frac{2}{3}$
(4)“a>0,b>0”是“$\frac{a}{b}+\frac{b}{a}≥2$”的充分不必要条件.
| A. | (1)(4) | B. | (2)(3) | C. | (1)(3) | D. | (3)(4) |
4.函数f(x)=|log2x|-x+1的零点个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
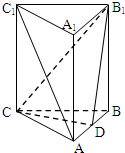 如图所示,在所有棱长都为2a的三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,D点为棱AB的中点.
如图所示,在所有棱长都为2a的三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,D点为棱AB的中点.