题目内容
19.已知在△ABC中,a2+c2-b2=ac,log4sinA+log4sinC=-1,△ABC的面积为$\sqrt{3}$(1)求∠B及b的长度;
(2)求a的长.
分析 由已知及余弦定理可得cosB=$\frac{1}{2}$,结合B的范围即可求得B,由对数运算法则及积化和差公式可得a=c,由三角形面积公式即可求得a,b的值.
解答 解:∵a2+c2-b2=ac,
∴由余弦定理可得:cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{ac}{2ac}$=$\frac{1}{2}$,
∴由B为内角,可得B=60°,
∵log4sinA+log4sinC=-1,
∴sinAsinC=$\frac{1}{4}$=-$\frac{1}{2}$[cos(A+C)-cos(A-C)],既有:-$\frac{1}{2}$-cos(A-C)=-$\frac{1}{2}$,可得:cos(A-C)=0,
可得:A=C,a=c,
∵ABC的面积S=$\frac{1}{2}$acsinB=$\frac{\sqrt{3}}{4}$ac=$\sqrt{3}$,
∴a=c=2,
所以:a=b=c=2,A=B=C=60°.
点评 本题主要考查了余弦定理,三角形面积公式,对数运算法则及积化和差公式的综合应用,属于基本知识的考查.

练习册系列答案
相关题目
7.对于正实数a,记Ma为满足下述条件的函数f(x)构成的集合:?x1,x2∈R且x2>x1,有-a(x2-x1)<f(x2)-f(x1)<a(x2-x1).下列结论中正确的是( )
| A. | 若f(x)∈M${\;}_{{a}_{1}}$,g(x)∈M${\;}_{{a}_{2}}$,则f(x)•g(x)∈M${\;}_{{a}_{1}{a}_{2}}$ | |
| B. | 若f(x)∈M${\;}_{{a}_{1}}$,g(x)∈M${\;}_{{a}_{2}}$,且g(x)≠0,则$\frac{f(x)}{g(x)}$∈M${\;}_{\frac{{a}_{1}}{{a}_{2}}}$ | |
| C. | 若f(x)∈M${\;}_{{a}_{1}}$,g(x)∈M${\;}_{{a}_{2}}$,则f(x)+g(x)∈M${\;}_{{a}_{1}+{a}_{2}}$ | |
| D. | 若f(x)∈M${\;}_{{a}_{1}}$,g(x)∈M${\;}_{{a}_{2}}$,且a1>a2,则f(x)-g(x)∈M${\;}_{{a}_{1}-{a}_{2}}$ |
14.哈六中高三学习雷锋志愿小组共有16人,其中一班、二班、三班、四班各4人,现在从中任选3人,要求这三人不能是同一个班级的学生,且在三班至多选1人,不同的选取法的种数为( )
| A. | 484 | B. | 472 | C. | 252 | D. | 232 |
4.函数f(x)=|log2x|-x+1的零点个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
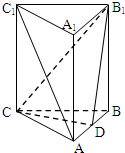 如图所示,在所有棱长都为2a的三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,D点为棱AB的中点.
如图所示,在所有棱长都为2a的三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,D点为棱AB的中点. 如图,为了测得河的宽度CD,在一岸边选定两点A、B,使A、B、D在同一直线上.现测得∠CAB=30°,∠CBA=75°,AB=120m,则河的宽度是60m.
如图,为了测得河的宽度CD,在一岸边选定两点A、B,使A、B、D在同一直线上.现测得∠CAB=30°,∠CBA=75°,AB=120m,则河的宽度是60m.