题目内容
【题目】对于定义域为![]() 的函数
的函数![]() ,若存在区间
,若存在区间![]() ,同时满足下列条件:①
,同时满足下列条件:①![]() 在
在![]() 上是单调的;②当定义域是
上是单调的;②当定义域是![]() 时,
时,![]() 的值域也是
的值域也是![]() ,则称
,则称![]() 为该函数的“和谐区间”.下列函数存在“和谐区间”的是( )
为该函数的“和谐区间”.下列函数存在“和谐区间”的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】BD
【解析】
由 “和谐区间”定义,结合每个函数进行判断,逐一证明函数存在或不存在“和谐区间”即可
对A,可知函数单调递增,则若定义域为![]() 时,值域为
时,值域为![]() ,故
,故![]() 不存在“和谐区间”;
不存在“和谐区间”;
对B,![]() ,可假设在
,可假设在![]() 存在“和谐区间”,函数为增函数,若定义域为
存在“和谐区间”,函数为增函数,若定义域为![]() 时,值域为
时,值域为![]() ,则
,则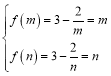 ,解得
,解得![]() (符合),
(符合),![]() (舍去),故函数存在“和谐区间”;
(舍去),故函数存在“和谐区间”;
对C,![]() ,对称轴为
,对称轴为![]() ,先讨论
,先讨论![]() 区间,函数为减函数,若定义域为
区间,函数为减函数,若定义域为![]() 时,值域为
时,值域为![]() ,则满足
,则满足![]() ,解得
,解得![]() ,故与题设矛盾;同理当
,故与题设矛盾;同理当![]() 时,应满足
时,应满足![]() ,解得
,解得![]() ,故无解,所以
,故无解,所以![]() 不存在“和谐区间”;
不存在“和谐区间”;
对D,![]() 为单增函数,则应满足
为单增函数,则应满足![]() ,可将解析式看作
,可将解析式看作![]() ,
,![]() ,由图可知,两函数图像有两个交点,则存在“和谐区间”
,由图可知,两函数图像有两个交点,则存在“和谐区间”
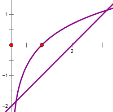
故选:BD

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】历史数据显示:某城市在每年的3月11日—3月15日的每天平均气温只可能是-5℃,-6℃,-7℃,-8℃中的一个,且等可能出现.
(Ⅰ)求该城市在3月11日—3月15日这5天中,恰好出现两次-5℃,一次-8℃的概率;
(Ⅱ)若该城市的某热饮店,随平均气温的变化所售热饮杯数如下表
平均气温t | -5℃ | -6℃ | -7℃ | -8℃ |
所售杯数y | 19 | 22 | 24 | 27 |
根据以上数据,求![]() 关于
关于![]() 的线性回归直线方程.
的线性回归直线方程.
(参考公式: ,
,![]() )
)

