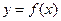题目内容
函数 .
.
(1)求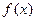 的解析式;
的解析式;
(2)求证:函数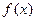 为奇函数;
为奇函数;
(3)若实数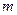 满足:
满足: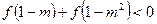 , 求
, 求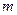 的取值范围
的取值范围
 .
.(1)求
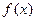 的解析式;
的解析式;(2)求证:函数
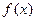 为奇函数;
为奇函数;(3)若实数
 满足:
满足: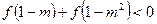 , 求
, 求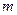 的取值范围
的取值范围(1)
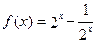 (2)
(2)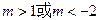
(1)令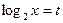 ,则
,则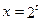 ,
,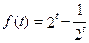 ,即
,即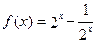
(2)函数定义域为R,对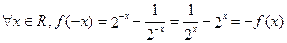 ,
,
函数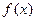 为奇函数
为奇函数
(3)首先需证明函数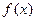 在R上是增函数(略)
在R上是增函数(略)
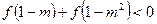

所以,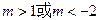
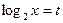 ,则
,则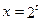 ,
,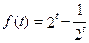 ,即
,即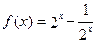
(2)函数定义域为R,对
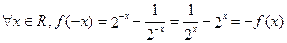 ,
,函数
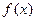 为奇函数
为奇函数(3)首先需证明函数
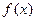 在R上是增函数(略)
在R上是增函数(略)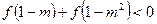

所以,
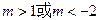

练习册系列答案
相关题目
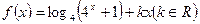 是偶函数.
是偶函数.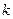 的值;
的值;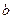 ,函数
,函数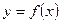 的图象与直线
的图象与直线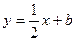 最多只有一个交点.
最多只有一个交点. 的长为
的长为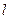 ,弦AP的长为
,弦AP的长为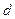 ,则函数
,则函数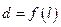 的图象大致是
的图象大致是 
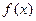
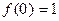
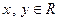
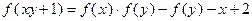 .
.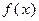 的解析式;
的解析式;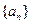 满足:
满足: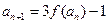 (
(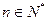 ),且
),且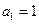 , 求数列
, 求数列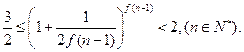
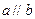 ,求实数
,求实数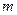 的值;
的值;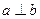 ,求实数
,求实数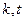 使得
使得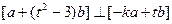 ,试求
,试求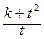 的最小值.
的最小值.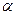 ,
,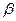 分别是关于
分别是关于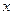 的方程
的方程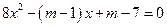 的两个根,且
的两个根,且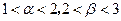 ,求实数
,求实数 的取值范围.
的取值范围.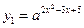 ,
,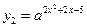 ,当
,当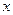 为何值时
为何值时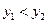 ?
?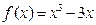 在
在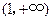 上的单调性并加以证明.
上的单调性并加以证明.