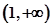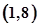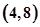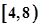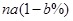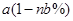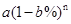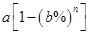题目内容
设函数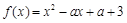 ,
,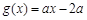 ,
,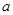 为常数,若存在
为常数,若存在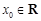 ,使得
,使得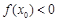 与
与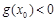 同时成立,则实数a的取值范围是 .
同时成立,则实数a的取值范围是 .
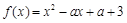 ,
,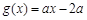 ,
,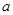 为常数,若存在
为常数,若存在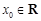 ,使得
,使得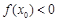 与
与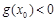 同时成立,则实数a的取值范围是 .
同时成立,则实数a的取值范围是 .
试题分析:因为f(x)<0有解需满足
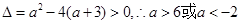 .
.当a>6时,g(x)<0的解为x<2,所以f(x)<0在x<2上有解即可.即f(x)在x<2上的最小值小于零即可.此时
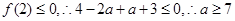 .当a<-2时,g(x)<0的解为x>2,所以只须f(x)<0在x>2上有解即可,即f(x)在x>2上的最小值小于零即可,也须满足
.当a<-2时,g(x)<0的解为x>2,所以只须f(x)<0在x>2上有解即可,即f(x)在x>2上的最小值小于零即可,也须满足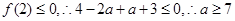 ,显然不成立.
,显然不成立.所以
 .
.点评:因为f(x)<0有解,所以
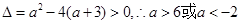 ,这样就把a的大致范围确定,然后讨论更有针对性,这是研究此类问题的一般方法,请认真体会.
,这样就把a的大致范围确定,然后讨论更有针对性,这是研究此类问题的一般方法,请认真体会.
练习册系列答案
相关题目
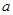 和
和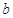 ,定义运算“﹡”:
,定义运算“﹡”: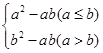 ,设
,设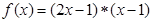 且关于
且关于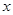 的方程
的方程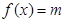 (
(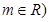 恰有三个互不相等的实根
恰有三个互不相等的实根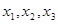 ,则
,则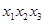 的取值范围是 。
的取值范围是 。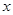 为实数,则
为实数,则 与
与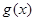 表示同一个函数的是 ( )
表示同一个函数的是 ( ) 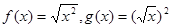

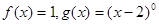

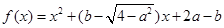 是偶函数,则函数图像与
是偶函数,则函数图像与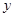 轴交点的纵坐标的最大值是( ).
轴交点的纵坐标的最大值是( ). },B={y|1
},B={y|1 },下列图形表示集合A到集合B的函数图形的是( )
},下列图形表示集合A到集合B的函数图形的是( )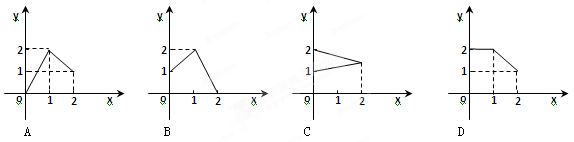

 (
( 为实数)有两个不相等的实数根,分别求:
为实数)有两个不相等的实数根,分别求: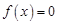 的根为一正一负,则求实数
的根为一正一负,则求实数 内,则求实数
内,则求实数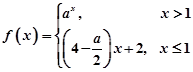 是R上的增函数,则实数
是R上的增函数,则实数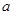 的取值范围为( )
的取值范围为( )