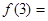题目内容
(本小题满分12分) 已知方程
 (
( 为实数)有两个不相等的实数根,分别求:
为实数)有两个不相等的实数根,分别求:
(Ⅰ)若方程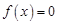 的根为一正一负,则求实数
的根为一正一负,则求实数 的取值范围;
的取值范围;
(Ⅱ)若方程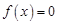 的两根都在
的两根都在 内,则求实数
内,则求实数 的取值范围
的取值范围

 (
( 为实数)有两个不相等的实数根,分别求:
为实数)有两个不相等的实数根,分别求:(Ⅰ)若方程
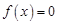 的根为一正一负,则求实数
的根为一正一负,则求实数 的取值范围;
的取值范围;(Ⅱ)若方程
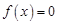 的两根都在
的两根都在 内,则求实数
内,则求实数 的取值范围
的取值范围 (Ⅰ)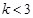 ;(Ⅱ)
;(Ⅱ)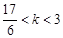 .
.
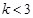 ;(Ⅱ)
;(Ⅱ)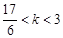 .
.试题分析:(1)判断上述方程的根的情况,只要看根的判别式△=b2-4ac的值加上韦达定理的符号就可以了.
(2)利用根与系数的关系以及f(-1),f(1),对称轴在(-1,1)内,确定两个根的取值情况.
解:(Ⅰ)由根与函数图像的关系,则方程
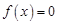 的根为一正一负
的根为一正一负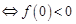 ,即
,即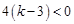 ,所以实数
,所以实数 的取值范围是
的取值范围是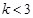 ;
;(Ⅱ)由
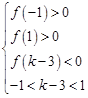 ,解之,
,解之,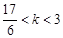 .
.点评:解决该试题的关键是能理解一元二次方程的根的正负与判别式韦达定理的关系的运用,以及两个根都在(-1,1)内,结合图像利用端点的函数值,以及判别式,对称轴来得到。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 =
=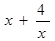
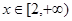 上是增函数;(2)求
上是增函数;(2)求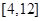 上的值域。
上的值域。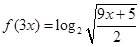 ,那么
,那么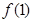 =_____________。
=_____________。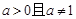 ,函数
,函数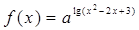 有最大值,则不等式
有最大值,则不等式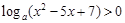 的解集为 .
的解集为 .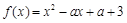 ,
,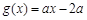 ,
,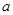 为常数,若存在
为常数,若存在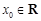 ,使得
,使得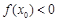 与
与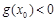 同时成立,则实数a的取值范围是 .
同时成立,则实数a的取值范围是 .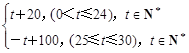 ;该商品的日销售量Q(件)与时间(天)的函数关系式为:
;该商品的日销售量Q(件)与时间(天)的函数关系式为: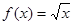 ,则
,则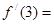 为( )
为( )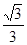
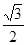
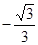
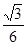
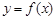 满足
满足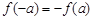 ,且
,且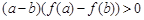
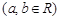 .若当
.若当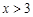 时不等式
时不等式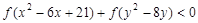 成立,则
成立,则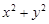 的取值范围是( )
的取值范围是( )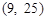
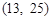
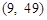
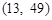
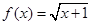 ,则
,则