题目内容
17.有一道解三角形的题目,因纸张破损有一个条件模糊不清,具体如下:“在△ABC中,已知$a=\sqrt{3}$,$B=\frac{π}{4}$,$A=\frac{π}{6}$(或$C=\frac{7π}{12}$),求b.”若破损处的条件为三角形的一个内角的大小,且答案提示$b=\sqrt{6}$.试在横线上将条件补充完整.分析 要把横线处补全,就要把$b=\sqrt{6}$作为已知条件求A和C的值,由a,B和b的值,根据正弦定理求出A,再由三角形的内角和定理求出C的度数即可得解.
解答 解:∵$a=\sqrt{3}$,$B=\frac{π}{4}$,$b=\sqrt{6}$.
∴由正弦定理可得:sinA=$\frac{asinB}{b}$=$\frac{\sqrt{3}×\frac{\sqrt{2}}{2}}{\sqrt{6}}$=$\frac{1}{2}$,
∵$\sqrt{3}<\sqrt{6}$,A<B,
∴解得:A=$\frac{π}{6}$,C=π-A-B=$\frac{7π}{12}$.
∵破损处的条件为三角形的一个内角的大小,故横线上的条件为:$A=\frac{π}{6}$(或$C=\frac{7π}{12}$).
故答案为:$A=\frac{π}{6}$(或$C=\frac{7π}{12}$).
点评 此题考查学生灵活运用正弦定理化简求值,灵活运用三角形内角和定理化简求值,把b的值看做已知条件求A或C的s值是解本题的基本思路,属于基础题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
8. 研究某设备的使用年限x与保养和维修费用y之间的关系,测得一组数据如下
研究某设备的使用年限x与保养和维修费用y之间的关系,测得一组数据如下
由数据可知y与x有明显的线性相关关系,附参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2-n{\overline{x}}^{2}}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$
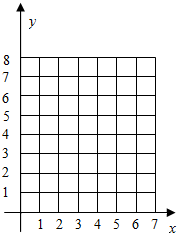
(1)将表中的数据画成散点图:
(2)试预测第7年的设备保养和维修费用.
 研究某设备的使用年限x与保养和维修费用y之间的关系,测得一组数据如下
研究某设备的使用年限x与保养和维修费用y之间的关系,测得一组数据如下| 年限x(年) | 2 | 3 | 4 | 5 | 6 |
| 保养和维修费用y(万元) | 3 | 3.5 | 5 | 6.5 | 7 |
(1)将表中的数据画成散点图:
(2)试预测第7年的设备保养和维修费用.
5.已知复数z=$\frac{2+i}{i^3}$,z的共轭复数是$\overline{z}$,则$\overline{z}$对应的点位于复平面内的( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
12.已知函数f(x)=$\frac{1}{2}$x2-2alnx+(a-2)x,对任意x1,x2∈(0,+∞),且当x1>x2时,f(x1)-ax1>f(x2)-ax2恒成立,则实数a的取值范围是( )
| A. | a>-$\frac{1}{2}$ | B. | a<-$\frac{1}{2}$ | C. | a≥-$\frac{1}{2}$ | D. | a≤-$\frac{1}{2}$ |
2.函数$y=\frac{{{{(x-1)}^0}}}{{\sqrt{|x|+x}}}$的定义域是( )
| A. | (0,+∞) | B. | (0,1)∪(1,+∞) | C. | (-∞,0) | D. | (-∞,-1)∪(0,+∞) |