题目内容
在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,若a=1,b=2,cosC=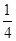 .求:
.求:
(1)△ABC的周长;
(2)cos(A-C)的值.
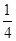 .求:
.求:(1)△ABC的周长;
(2)cos(A-C)的值.
(1)5(2)

(1)因为c2=a2+b2-2abcosC=1+4-4×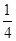 =4.
=4.
所以c=2.所以△ABC的周长为a+b+c=1+2+2=5.
(2)因为cosC=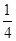 ,所以sinC=
,所以sinC=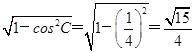 .
.
所以sinA=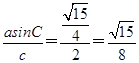 .因为a<c,所以A<C,故A为锐角,
.因为a<c,所以A<C,故A为锐角,
所以cosA=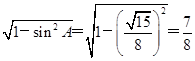 .
.
所以cos(A-C)=cosAcosC+sinAsinC=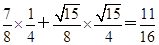
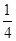 =4.
=4.所以c=2.所以△ABC的周长为a+b+c=1+2+2=5.
(2)因为cosC=
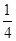 ,所以sinC=
,所以sinC=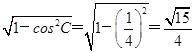 .
.所以sinA=
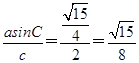 .因为a<c,所以A<C,故A为锐角,
.因为a<c,所以A<C,故A为锐角,所以cosA=
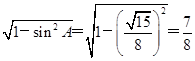 .
.所以cos(A-C)=cosAcosC+sinAsinC=
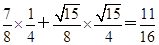

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
 .求:
.求: 的值.
的值.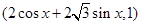 ,n=
,n=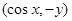 ,满足
,满足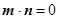 .
. ,并求
,并求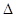 ABC的三个内角A,B,C对应的边长,
ABC的三个内角A,B,C对应的边长,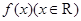 的最大值是
的最大值是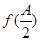 ,且a=2,求b+c的取值范围.
,且a=2,求b+c的取值范围.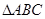 中,
中,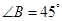 ,
,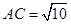 ,
,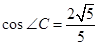 点
点 是
是 的中点, 求
的中点, 求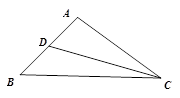
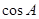 的值和中线
的值和中线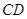 的长
的长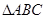 中,角
中,角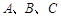 所对的边分别为
所对的边分别为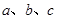 ,已知
,已知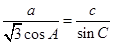 ,
,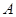 的大小;(2)若
的大小;(2)若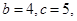 求
求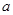 的值.
的值.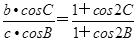 ,试判断△ABC的形状.
,试判断△ABC的形状. 的三内角
的三内角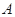 、
、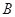 、
、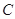 所对边的边长分别为
所对边的边长分别为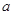 、
、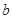 、
、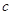 ,且
,且 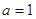 ,
,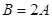 ,则
,则
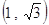
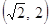
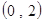
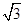 ,则c等于( )
,则c等于( )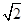 (D)1
(D)1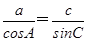 ,则A=________.
,则A=________.