题目内容
已知斜率为2的直线l过抛物线y2=ax(a>0)的焦点F,且与y轴相交于点A,若△OAF(O为坐标原点)的面积为4,则抛物线方程为________.
y2=8x
依题意得,OF=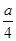 ,又直线l的斜率为2,可知AO=2OF=
,又直线l的斜率为2,可知AO=2OF=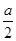 ,△AOF的面积等于
,△AOF的面积等于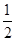 ·AO·OF=
·AO·OF=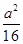 =4,则a2=64.又a>0,所以a=8,该抛物线的方程是y2=8x.
=4,则a2=64.又a>0,所以a=8,该抛物线的方程是y2=8x.
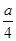 ,又直线l的斜率为2,可知AO=2OF=
,又直线l的斜率为2,可知AO=2OF=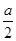 ,△AOF的面积等于
,△AOF的面积等于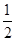 ·AO·OF=
·AO·OF=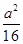 =4,则a2=64.又a>0,所以a=8,该抛物线的方程是y2=8x.
=4,则a2=64.又a>0,所以a=8,该抛物线的方程是y2=8x.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
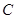 :
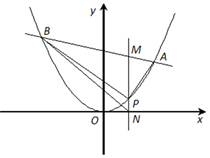
: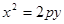 过点
过点 ,直线
,直线 交
交 ,
, 两点,过点
两点,过点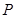 且平行于
且平行于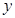 轴的直线分别与直线
轴的直线分别与直线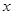 轴相交于点
轴相交于点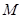 ,
, .
.
 的值;
的值; ,当直线
,当直线 与△
与△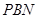 的面积相等?若存在,求出点
的面积相等?若存在,求出点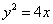 的焦点到双曲线
的焦点到双曲线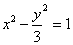 的渐近线的距离是( )
的渐近线的距离是( )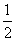

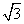
 的焦点F作直线AB,CD与抛物线交于A、B、C、D四点,且
的焦点F作直线AB,CD与抛物线交于A、B、C、D四点,且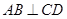 ,则
,则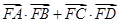 的最大等于 ( )
的最大等于 ( )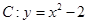 ,过原点的动直线
,过原点的动直线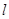 交抛物线
交抛物线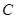 于
于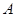 、
、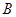 两点,
两点,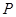 是
是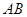 的中点,设动点
的中点,设动点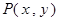 ,则
,则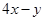 的最大值是( )
的最大值是( )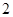
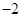
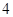
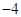
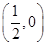 的距离比到y轴的距离大
的距离比到y轴的距离大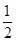 .记点P的轨迹为曲线C.
.记点P的轨迹为曲线C.