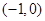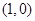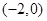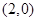题目内容
求满足下列条件的抛物线的标准方程,并求对应抛物线的准线方程.
(1)过点(-3,2);
(2)焦点在直线x-2y-4=0上.
(1)过点(-3,2);
(2)焦点在直线x-2y-4=0上.
(1)y2=-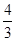 x或x2=
x或x2=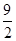 y,前者的准线方程是x=
y,前者的准线方程是x=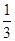 ,后者的准线方程是y=-
,后者的准线方程是y=-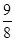 .(2)所求抛物线的方程为y2=16x或x2=-8y,对应的准线方程分别是x=-4,y=2.
.(2)所求抛物线的方程为y2=16x或x2=-8y,对应的准线方程分别是x=-4,y=2.
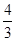 x或x2=
x或x2=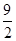 y,前者的准线方程是x=
y,前者的准线方程是x=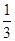 ,后者的准线方程是y=-
,后者的准线方程是y=-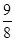 .(2)所求抛物线的方程为y2=16x或x2=-8y,对应的准线方程分别是x=-4,y=2.
.(2)所求抛物线的方程为y2=16x或x2=-8y,对应的准线方程分别是x=-4,y=2.(1)设所求抛物线的方程为y2=-2px或x2=2py(p>0).
∵过点(-3,2),∴4=-2p(-3)或9=2p·2.∴p=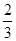 或p=
或p=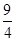 .∴所求抛物线的方程为y2=-
.∴所求抛物线的方程为y2=-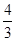 x或x2=
x或x2=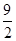 y,前者的准线方程是x=
y,前者的准线方程是x=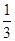 ,后者的准线方程是y=-
,后者的准线方程是y=-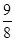 .
.
(2)令x=0得y=-2,令y=0得x=4,∴抛物线的焦点为(4,0)或(0,-2).当焦点为(4,0)时,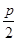 =4,∴p=8,此时抛物线的方程为y2=16x;焦点为(0,-2)时,
=4,∴p=8,此时抛物线的方程为y2=16x;焦点为(0,-2)时,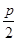 =2,∴p=4,此时抛物线的方程为x2=-8y.∴所求抛物线的方程为y2=16x或x2=-8y,对应的准线方程分别是x=-4,y=2.
=2,∴p=4,此时抛物线的方程为x2=-8y.∴所求抛物线的方程为y2=16x或x2=-8y,对应的准线方程分别是x=-4,y=2.
∵过点(-3,2),∴4=-2p(-3)或9=2p·2.∴p=
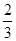 或p=
或p=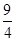 .∴所求抛物线的方程为y2=-
.∴所求抛物线的方程为y2=-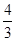 x或x2=
x或x2=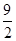 y,前者的准线方程是x=
y,前者的准线方程是x=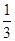 ,后者的准线方程是y=-
,后者的准线方程是y=-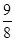 .
.(2)令x=0得y=-2,令y=0得x=4,∴抛物线的焦点为(4,0)或(0,-2).当焦点为(4,0)时,
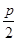 =4,∴p=8,此时抛物线的方程为y2=16x;焦点为(0,-2)时,
=4,∴p=8,此时抛物线的方程为y2=16x;焦点为(0,-2)时,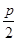 =2,∴p=4,此时抛物线的方程为x2=-8y.∴所求抛物线的方程为y2=16x或x2=-8y,对应的准线方程分别是x=-4,y=2.
=2,∴p=4,此时抛物线的方程为x2=-8y.∴所求抛物线的方程为y2=16x或x2=-8y,对应的准线方程分别是x=-4,y=2.
练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
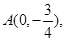 点
点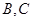 分别是
分别是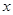 轴和
轴和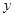 轴上的动点,且
轴上的动点,且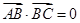 ,动点
,动点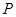 满足
满足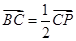 ,设动点
,设动点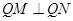 ,过M,N两点分别作曲线E的切线,记两切线的交点为
,过M,N两点分别作曲线E的切线,记两切线的交点为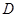 ,求
,求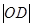 的最小值.
的最小值.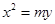

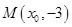 到焦点的距离为
到焦点的距离为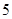 ,则实数
,则实数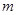 的值为( )
的值为( )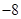

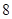
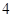
 x2+2上一动点P(x,y),则y+|PQ|最小值为( )
x2+2上一动点P(x,y),则y+|PQ|最小值为( )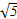
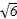
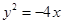 ,则它的焦点坐标为( )
,则它的焦点坐标为( )