题目内容
如图，正三棱柱ABC-A1B1C1的各棱长都相等，M、E分别是AB和AB1的中点，点F在BC上且满足BF：FC=1：3．
（1）求证：BB1∥平面EFM；
（2）求四面体M-BEF的体积．
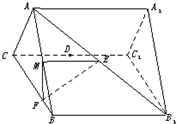
（1）求证：BB1∥平面EFM；
（2）求四面体M-BEF的体积．
（1）证明：连结EM、MF，
∵M、E分别是正三棱柱的棱AB和AB1的中点，
∴BB1∥ME，
又BB1?平面EFM，ME?平面EFM，
∴BB1∥平面EFM．
（2）正三棱柱中B1B⊥底面ABC，
由（1）BB1∥ME，
∴ME⊥平面MBF，
根据条件得出BF=1，BM=2，∠MBF=60°，
∴S△BMF=
，
又EM=2，
因此VM-BEF=VE-MBF=
S△BMF•EM=
．
∵M、E分别是正三棱柱的棱AB和AB1的中点，
∴BB1∥ME，
又BB1?平面EFM，ME?平面EFM，
∴BB1∥平面EFM．
（2）正三棱柱中B1B⊥底面ABC，
由（1）BB1∥ME，
∴ME⊥平面MBF，
根据条件得出BF=1，BM=2，∠MBF=60°，
∴S△BMF=
| ||
| 2 |
又EM=2，
因此VM-BEF=VE-MBF=
| 1 |
| 3 |
| ||
| 3 |
练习册系列答案
小学课时作业全通练案系列答案
相关题目
