题目内容
将圆x2+y2 -2x-4y+1=0平分的直线是
| A. x+y-1=0 | B.x+y+3=0 | C.x-y+1=0 | D.x-y+3=0 |
C
解析试题分析:易知圆x2+y2 -2x-4y+1=0的圆心为: ,若直线平分圆,则直线一定过圆心,只有选项C中的直线过圆心,因此选C。
,若直线平分圆,则直线一定过圆心,只有选项C中的直线过圆心,因此选C。
考点:圆的一般式方程;圆的简单性质。
点评:过圆心的直线平分圆。属于基础题型。

练习册系列答案
相关题目
直线 与圆
与圆 相交于M、N两点,若
相交于M、N两点,若 ,则k的取值范围为( )
,则k的取值范围为( )
A. | B. | C. | D.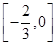 |
两圆相交于点 ,两圆的圆心均在直线
,两圆的圆心均在直线 上,则
上,则 的值为( )
的值为( )
A. | B. | C. | D. |
设 ,
, ,若直线
,若直线 与圆
与圆 相切,则
相切,则 的取值范
的取值范
围是( )
A. | B. |
C. | D. |
若 ,则直线
,则直线 被圆
被圆 所截得的弦长为( )
所截得的弦长为( )
A. | B.1 | C. | D. |
若圆 始终平分圆
始终平分圆 的周长, 则a、b应满足的关系式是
的周长, 则a、b应满足的关系式是
A. 0 0 | B. 0 0 |
C. 0 0 | D. 0 0 |
若点P(1,1)为圆 的弦MN的中点,则弦MN所在直线的方程为( )
的弦MN的中点,则弦MN所在直线的方程为( )
A. | B. |
C. | D. |
直线 绕原点按顺时针方向旋转
绕原点按顺时针方向旋转 所得直线与圆
所得直线与圆 的位置关系是( ).
的位置关系是( ).
| A.直线与圆相切 | B.直线与圆相交但不过圆心 |
| C.直线与圆相离 | D.直线过圆心 |
以下叙述正确的是( )
| A.平面直角坐标系下的每条直线一定有倾斜角与法向量,但是不一定都有斜率; |
| B.平面上到两个定点的距离之和为同一个常数的轨迹一定是椭圆; |
C.直线 上有且仅有三个点到圆 上有且仅有三个点到圆 的距离为2; 的距离为2; |
D.点 是圆 是圆 上的任意一点,动点 上的任意一点,动点 分 分 ( ( 为坐标原点)的比为 为坐标原点)的比为 ,那么 ,那么 的轨迹是有可能是椭圆. 的轨迹是有可能是椭圆. |