题目内容
若点P（1，1）为圆
的弦MN的中点，则弦MN所在直线的方程为（ ）
A． | B． |
C． | D． |
D
解析试题分析：由题意可知弦MN所在直线过点P（1，1），因此要求弦MN所在直线的方程只需求出直线的斜率即可。设圆的圆心为O,由直线MN与OP垂直就可求出直线MN的斜率。
考点：本题考查直线方程的点斜式
和斜率公式
点评：直线与圆往往结合到一块考查。我们要熟练掌握直线方程的五种形式，及每一种形式的特点和应用前提。例如直线方程的点斜式的特点是一点一斜率；应用前提是斜率存在。
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
过定点
作直线
，使与抛物线
有且仅有一个公共点，这样的直线共有（ ）
| A．1条 | B．2条 | C．3条 | D．4条 |
圆C：x2＋y2＋2x＋4y－3=0上到直线
：x＋y＋1=0的距离为
的点共有( )
| A．１个 | B．２个 | C．３个 | D．４个 |
将圆x2+y2 -2x-4y+1=0平分的直线是
| A． x+y-1=0 | B．x+y+3=0 | C．x-y+1=0 | D．x-y+3=0 |
由直线
上的一点向圆
引切线,则切线长的最小值为( )
| A．1 | B． | C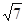． | D．3 |
若点
为圆
的弦
的中点，则直线的方程为（ ）
A． | B． |
C． | D． |
若直线
与曲线
有公共点，则
的取值范围是（ ）
A． | B． |
C． | D． |
已知圆
与直线
及
都相切，圆心在直线
上，则圆的方程为（ ）
A． | B． |
C． | D． |
已知圆心在x轴上，半径是5且以A(5，4)为中点的弦长是2
，则这个圆的方程是（ ）
| A．(x－3)2+y2=25 | B．(x－7)2+y2=25 |
| C．(x±3)2+y2=25 | D．(x－3)2+y2=25或(x－7)2+y2=25 |