设,,若直线与圆相切,则的取值范围是( )A． B． C． D．题目和参考答案——青夏教育精英家教网—

题目内容

设,,若直线与圆相切,则的取值范
围是（　　）

A．	B．
C．	D．

解析试题分析：因为直线与圆相切,所以，即，所以，所以的取值范
围是。
考点：圆的简单性质；点到直线的距离公式；基本不等式。
点评：做本题的关键是灵活应用基本不等式，注意基本不等式应用的前提条件：一正二定三相等。

练习册系列答案

全优备考卷系列答案

相关题目

由直线上的一点向圆引切线，则切线长的最小值（）

A．	B．
C．	D．

若点为圆的弦的中点，则弦所在直线方程为（　　）

圆C：x²＋y²＋2x＋4y－3=0上到直线：x＋y＋1=0的距离为的点共有(　　)

已知圆心为C（6，5），且过点B（3，6）的圆的方程为

A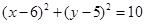．	B．
C．	D．

将圆x²+y² -2x-4y+1=0平分的直线是

若点为圆的弦的中点，则直线的方程为（）

A．	B．
C．	D．

动点在圆x²＋y²=1上移动时，它与定点B（3，0）连线的中点轨迹方程是（）

A．（x＋3)²＋y²=4	B．（x－3)²＋y²=1
C．（2x－3)²＋4y²=1	D．（x＋)²＋y²=

点在圆的内部，则的取值范围是（　　）

A．	B．
C．或	D．

试题分类