题目内容
若圆 始终平分圆
始终平分圆 的周长, 则a、b应满足的关系式是
的周长, 则a、b应满足的关系式是
A. 0 0 | B. 0 0 |
C. 0 0 | D. 0 0 |
B
解析试题分析:∵圆(x-a)2+(y-b)2=b2+1始终平分(x+1)2+(y+1)2=4的周长
∴两圆交点的直线过(x+1)2+(y+1)2=4的圆心(-1,-1)
两圆方程相减可得:(2+2a)x+(2+2b)y-a2-1=0,得到相交弦所在直线,然后
将(-1,-1)代入可得-2-2a-2-2b-a2-1=0,即5+2a+2b+a2=0
故选B
考点:本题主要考查了圆与圆的位置关系,考查学生分析解决问题的能力,属于中档题.
点评:解决该试题的关键是根据圆(x-a)2+(y-b)2=b2+1始终平分(x+1)2+(y+1)2=4的周长,可得两圆交点的直线过(x+1)2+(y+1)2=4的圆心(-1,-1),两圆相减可得公共弦,将(-1,-1)代入可得结论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知圆C: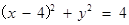 ,从动圆M:
,从动圆M: 上的动点P向圆C引切线,切点分别是E,F,则
上的动点P向圆C引切线,切点分别是E,F,则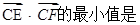 ( )
( )
A. | B. | C. | D. |
若点 为圆
为圆 的弦
的弦 的中点,则弦
的中点,则弦 所在直线方程为( )
所在直线方程为( )
A. | B. | C. | D. |
已知圆心为C(6,5),且过点B(3,6)的圆的方程为
A.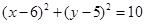 | B. |
C. | D. |
将圆x2+y2 -2x-4y+1=0平分的直线是
| A. x+y-1=0 | B.x+y+3=0 | C.x-y+1=0 | D.x-y+3=0 |
已知 ,点
,点
 是圆
是圆 内一点,直线
内一点,直线 是以点
是以点 为中点的弦所在的直线,直线
为中点的弦所在的直线,直线 的方程是
的方程是 ,则下列结论正确的是( )
,则下列结论正确的是( )
A. ,且 ,且 与圆相交 与圆相交 | B. ,且 ,且 与圆相切 与圆相切 |
C. ,且 ,且 与圆相离 与圆相离 | D. ,且 ,且 与圆相离 与圆相离 |
若点 为圆
为圆 的弦
的弦 的中点,则直线
的中点,则直线 的方程为( )
的方程为( )
A. | B. |
C. | D. |
过点(1,2)总可作两条直线与圆 相切,则实数
相切,则实数 的取值范围是( )
的取值范围是( )
A. | B. |
C. 或 或 | D.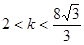 或 或 |
若P(2,-1)为圆(x-1)2+y2=25的弦AB的中点,则直线AB的方程是 ( )
| A.x-y-3=0 | B.2x+y-3=0 |
| C.x+y-1=0 | D.2x-y-5=0 |