题目内容
设椭圆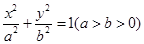 的四个顶点A、B、C、D, 若菱形ABCD的内切圆恰好经过椭圆的焦点, 则椭圆的离心率为 __ .
的四个顶点A、B、C、D, 若菱形ABCD的内切圆恰好经过椭圆的焦点, 则椭圆的离心率为 __ .
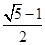
解析试题分析:由题意,不妨设点A(a,0),B(0,b),则直线AB的方程为: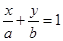 ,即bx+ay-ab=0。
,即bx+ay-ab=0。
∵菱形ABCD的内切圆恰好过焦点,∴原点到直线AB的距离为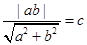 ,
,
∴a2b2=c2(a2+b2),∴a2(a2-c2)=c2(2a2-c2),∴a4-3a2c2+c4=0,∴e4-3e2+1=0,
解得e2=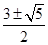 ,∵0<e<1,∴e=
,∵0<e<1,∴e=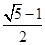 。
。
考点:椭圆的几何性质,点到直线的距离。
点评:中档题,解题的关键是利用菱形ABCD的内切圆恰好过焦点,得到原点到直线AB的距离等于半焦距,确定得到a,b,c的关系。

练习册系列答案
相关题目
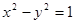 与圆
与圆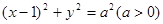 恰有三个不同的公共点,则
恰有三个不同的公共点,则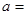 .
.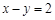 与抛物线
与抛物线 交于
交于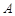 、
、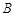 两点,则线段
两点,则线段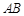 的中点坐标是______.
的中点坐标是______.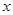 轴上,中心在原点,一条渐进线为
轴上,中心在原点,一条渐进线为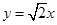 ,点
,点 在双曲线上,则双曲线的标准方程是 .
在双曲线上,则双曲线的标准方程是 .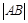 为C的实轴长的2倍,则C的离心率为_________.
为C的实轴长的2倍,则C的离心率为_________.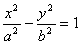
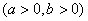 的渐近线与圆
的渐近线与圆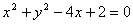 有公共点,则该双曲线的离心率的取值范围是___________.
有公共点,则该双曲线的离心率的取值范围是___________. 的焦点F的直线l与抛物线在第一象限的交点为A,直线l与抛物线的准线的交点为B,点A在抛物线的准线上的射影为C,若
的焦点F的直线l与抛物线在第一象限的交点为A,直线l与抛物线的准线的交点为B,点A在抛物线的准线上的射影为C,若 ,
, ,则抛物线的方程为 .
,则抛物线的方程为 . 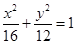 上的点到直线
上的点到直线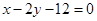 的距离的最小值为 。
的距离的最小值为 。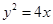 的焦点作直线
的焦点作直线 交抛物线于
交抛物线于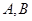 两点,若线段
两点,若线段 中点的横坐标为3,则
中点的横坐标为3,则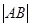 等于___________.
等于___________.