题目内容
9.已知圆M过C(1,-1),D(-1,1)两点,且圆心M在x+y-2=0上.(Ⅰ)求圆M的方程;
(Ⅱ)设P是直线3x+4y+8=0上的动点,PA,PB是圆M的两条切线,A,B为切点,求四边形PAMB面积的最小值.
分析 (1)设出圆的标准方程,利用圆M过两点C(1,-1)、D(-1,1)且圆心M在直线x+y-2=0上,建立方程组,即可求圆M的方程;
(2)四边形PAMB的面积为S=2$\sqrt{|PM{|}^{2}-4}$,因此要求S的最小值,只需求|PM|的最小值即可,在直线3x+4y+8=0上找一点P,使得|PM|的值最小,利用点到直线的距离公式,即可求得结论.
解答 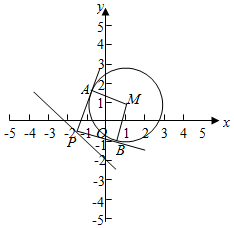 解:(1)设圆M的方程为:(x-a)2+(y-b)2=r2(r>0),
解:(1)设圆M的方程为:(x-a)2+(y-b)2=r2(r>0),
根据题意得$\left\{\begin{array}{l}{(1-a)^{2}+(-1-b)^{2}={r}^{2}}\\{(-1-a)^{2}+(1-b)^{2}={r}^{2}}\\{a+b-2=0}\end{array}\right.$,解得:a=b=1,r=2,
故所求圆M的方程为:(x-1)2+(y-1)2=4;
(2)由题知,四边形PAMB的面积为S=S△PAM+S△PBM=$\frac{1}{2}$(|AM||PA|+|BM||PB|).
又|AM|=|BM|=2,|PA|=|PB|,所以S=2|PA|,
而|PA|2=|PM|2-|AM|2=|PM|2-4,
即S=2$\sqrt{|PM{|}^{2}-4}$.
因此要求S的最小值,只需求|PM|的最小值即可,即在直线3x+4y+8=0上找一点P,使得|PM|的值最小,
所以|PM|min=$\frac{3+4+8}{5}$=3,所以四边形PAMB面积的最小值为2$\sqrt{|PM{|}^{2}-4}$=2$\sqrt{5}$.
点评 本题考查圆的标准方程,考查四边形面积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.抛掷一枚质地均匀的硬币,如果连续抛掷2011次,那么第2010次出现正面朝上的概率是( )
| A. | $\frac{1}{2010}$ | B. | $\frac{1}{2011}$ | C. | $\frac{2010}{2011}$ | D. | $\frac{1}{2}$ |
17.双曲线$\frac{x^2}{a^2}-\frac{y^2}{3}$=1(a>0)有一个焦点与抛物线y2=8x的焦点重合,则双曲线的渐近线方程为( )
| A. | y=±$\frac{1}{2}$x | B. | y=±2x | C. | y=±$\frac{{\sqrt{3}}}{3}$x | D. | y=±$\sqrt{3}$x |
4.已知集合D={x|$\frac{24-x}{x-9}$>0},若a,b∈D,且$\frac{1}{a}$+$\frac{1}{2b}$=$\frac{1}{12}$,则9a•3b的最小值为354.
1.化简复数$\frac{1}{{{{(1-i)}^2}}}$(其中i为虚数单位)所得结果为( )
| A. | $\frac{i}{2}$ | B. | -$\frac{i}{2}$ | C. | i | D. | -i |