题目内容
如果a<0,b<0,则必有( )
| A.a3+b3≥ab2+a2b | B.a3+b3≤ab2+a2b |
| C.a3+b3>ab2+a2b | D.a3+b3<ab2+a2b |
B
(a3+b3)-(ab2+a2b)
=(a3-ab2)-(a2b-b3)
=a(a2-b2)-b(a2-b2)
=(a2-b2)(a-b)
=(a-b)2(a+b),
由于a<0,b<0,所以(a-b)2≥0,a+b<0,
于是(a3+b3)-(ab2+a2b)≤0,
故a3+b3≤ab2+a2b.
=(a3-ab2)-(a2b-b3)
=a(a2-b2)-b(a2-b2)
=(a2-b2)(a-b)
=(a-b)2(a+b),
由于a<0,b<0,所以(a-b)2≥0,a+b<0,
于是(a3+b3)-(ab2+a2b)≤0,
故a3+b3≤ab2+a2b.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 恒成立,则n的最大值为( ).
恒成立,则n的最大值为( ). a∨b=
a∨b=
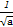 +
+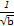 +
+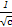 ≤a+b+c”的( )
≤a+b+c”的( )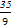 ≤a≤-1
≤a≤-1 +btan
+btan 的图像恒在
的图像恒在 轴上方,则
轴上方,则 +
+ 的最大值是________.
的最大值是________.