题目内容
设a,b∈R,定义运算“∧”和“∨”如下:
a∧b= a∨b=
a∨b=
若正数a,b,c,d满足ab≥4,c+d≤4,则( )
a∧b=
 a∨b=
a∨b=
若正数a,b,c,d满足ab≥4,c+d≤4,则( )
| A.a∧b≥2,c∧d≤2 | B.a∧b≥2,c∨d≥2 |
| C.a∨b≥2,c∧d≤2 | D.a∨b≥2,c∨d≥2 |
C
根据题意知,a∧b表示a,b中较小的,a∨b表示a,b中较大的.因为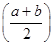 2≥ab≥4,所以a+b≥4.又因为a,b为正数,所以a,b中至少有一个大于或等于2,所以a∨b≥2.因为c+d≤4,c,d为正数,所以c,d中至少有一个小于或等于2,所以c∧d≤2.
2≥ab≥4,所以a+b≥4.又因为a,b为正数,所以a,b中至少有一个大于或等于2,所以a∨b≥2.因为c+d≤4,c,d为正数,所以c,d中至少有一个小于或等于2,所以c∧d≤2.
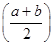 2≥ab≥4,所以a+b≥4.又因为a,b为正数,所以a,b中至少有一个大于或等于2,所以a∨b≥2.因为c+d≤4,c,d为正数,所以c,d中至少有一个小于或等于2,所以c∧d≤2.
2≥ab≥4,所以a+b≥4.又因为a,b为正数,所以a,b中至少有一个大于或等于2,所以a∨b≥2.因为c+d≤4,c,d为正数,所以c,d中至少有一个小于或等于2,所以c∧d≤2.
练习册系列答案
相关题目
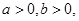 且
且 ,若
,若 恒成立,
恒成立, 的最小值;(2)若
的最小值;(2)若 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. +
+ +…+
+…+ <
< .
. 的不等式
的不等式 对于一切实数
对于一切实数 ”的
”的