题目内容
(本小题满分14分)
设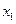 与
与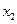 分别是实系数方程
分别是实系数方程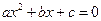 和
和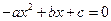 的一个根,且
的一个根,且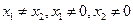 ,求证:方程
,求证:方程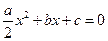 有仅有
有仅有 一根介于
一根介于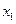 和
和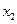 之间.
之间.
解:令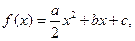 由题意可知
由题意可知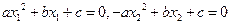
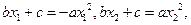

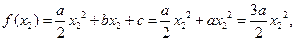 因为
因为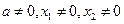
∴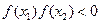 ,即方程
,即方程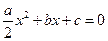 有仅有一根介于
有仅有一根介于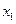 和
和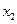 之间.
之间.
解析

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
题目内容
(本小题满分14分)
设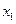 与
与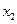 分别是实系数方程
分别是实系数方程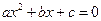 和
和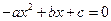 的一个根,且
的一个根,且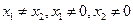 ,求证:方程
,求证:方程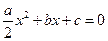 有仅有
有仅有 一根介于
一根介于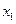 和
和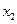 之间.
之间.
解:令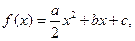 由题意可知
由题意可知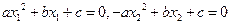
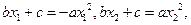

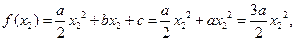 因为
因为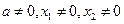
∴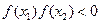 ,即方程
,即方程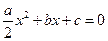 有仅有一根介于
有仅有一根介于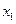 和
和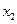 之间.
之间.
解析

 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案