题目内容
已知A(1,3),B(5,-2),在x轴上有一点P,若||AP|-|BP||最大,则P点坐标是______.
设B关于x轴的对称点为C
∵B的坐标为(5,-2),∴C坐标为(5,2)
延长AC交x轴于点P0,可得
当P与P0不重合时,
在△PAC中,||AP|-|CP||<|AC|=||AP0|-|CP0||
从而得出||AP|-|BP||=||AP|-|CP||<||AP0|-|CP0||
当P与P0重合时,||AP|-|BP||=||AP0|-|CP0||=|AC|
∴当动点P与P0重合时,||AP|-|BP||最大,最大值为A、C的距离
直线AC方程为
=
,化简得y=-
x+
令y=0,得x=13,可得P0的坐标为(13,0)
故答案为:(13,0)

∵B的坐标为(5,-2),∴C坐标为(5,2)
延长AC交x轴于点P0,可得
当P与P0不重合时,
在△PAC中,||AP|-|CP||<|AC|=||AP0|-|CP0||
从而得出||AP|-|BP||=||AP|-|CP||<||AP0|-|CP0||
当P与P0重合时,||AP|-|BP||=||AP0|-|CP0||=|AC|
∴当动点P与P0重合时,||AP|-|BP||最大,最大值为A、C的距离
直线AC方程为
| y-3 |
| 2-3 |
| x-1 |
| 5-1 |
| 1 |
| 4 |
| 13 |
| 4 |
令y=0,得x=13,可得P0的坐标为(13,0)
故答案为:(13,0)


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
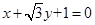 被圆
被圆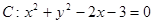 截得的弦长为 .
截得的弦长为 .