题目内容
已知点A(1,1),B(2,2),C(4,0),D(
,
),点P在线段CD垂直平分线上,求:
(1)线段CD垂直平分线方程;
(2)|PA|2+|PB|2取得最小值时P点的坐标.
| 12 |
| 5 |
| 16 |
| 5 |
(1)线段CD垂直平分线方程;
(2)|PA|2+|PB|2取得最小值时P点的坐标.
(1)由C(4,0),D(
,
),
得线段CD的中点M(
,
),kCD=
=-2,
∴线段CD的垂直平分线的斜率为
,
∴线段CD垂直平分线方程为:y-
=
(x-
),即x-2y=0;
(2)设P(2t,t),
则)|PA|2+|PB|2=(2t-1)2+(t-1)2+(2t-2)2+(t-2)2=10t2-18t+10.
当t=
时,|PA|2+|PB|2取得最小值,即P(
,
).
| 12 |
| 5 |
| 16 |
| 5 |
得线段CD的中点M(
| 16 |
| 5 |
| 8 |
| 5 |
| ||
|
∴线段CD的垂直平分线的斜率为
| 1 |
| 2 |
∴线段CD垂直平分线方程为:y-
| 8 |
| 5 |
| 1 |
| 2 |
| 16 |
| 5 |
(2)设P(2t,t),
则)|PA|2+|PB|2=(2t-1)2+(t-1)2+(2t-2)2+(t-2)2=10t2-18t+10.
当t=
| 9 |
| 10 |
| 9 |
| 5 |
| 9 |
| 10 |

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
 与曲线
与曲线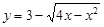 有公共点,则
有公共点,则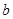 的取值范围是 .
的取值范围是 .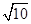 .
.