题目内容
【题目】 设f(x)、g(x)分别是定义在R上的奇函数和偶函数，当x＜0时，f′(x)·g(x)＋f(x)·g′(x)＞0，且f(－3)·g(－3)＝0，则不等式f(x)·g(x)＜0的解集是( )
A. (－3,0)∪(3，＋∞)
B. (－3,0)∪ (0,3)
C. (－∞，－3)∪(3，＋∞)
D. (－∞，－3)∪(0,3)
【答案】D
【解析】
试题设F（x）="f" （x）g（x），当x＜0时，∵F′（x）=f′（x）g（x）+f （x）g′（x）＞0．∴F（x）在当x＜0时为增函数．
∵F（-x）="f" （-x）g （-x）="-f" （x）g （x）=-F（x）．
故F（x）为（-∞，0）∪（0，+∞）上的奇函数．
∴F（x）在（0，∞）上亦为增函数．
已知f(－3)·g(－3)＝0，必有F（-3）=F（3）=0．
构造如图的F（x）的图象，
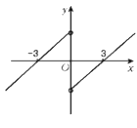
可知F（x）＜0的解集为x∈（-∞，-3）∪（0，3）．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
【题目】（本题满分12分）
今年十一黄金周，记者通过随机询问某景区110名游客对景区的服务是否满意，得到如下的列联表：
性别与对景区的服务是否满意 单位：名
男 | 女 | 总计 | |
满意 | 50 | 30 | 80 |
不满意 | 10 | 20 | 30 |
总计 | 60 | 50 | 110 |
（1）从这50名女游客中按对景区的服务是否满意采取分层抽样，抽取一个容量为5的样本，问样本中满意与不满意的女游客各有多少名？
（2）从（1）中的5名女游客样本中随机选取两名作深度访谈，求选到满意与不满意的女游客各一名的概率；
（3）根据以上列联表，问有多大把握认为“游客性别与对景区的服务满意”有关
注：
临界值表：
P( | 0.05 | 0.025 | 0.010 | 0.005 |
| 3.841 | 5.024 | 6.635 | 7.879 |
【题目】为了研究高中学生对乡村音乐的态度（喜欢和不喜欢两种态度）与性别的关系，运用2×2列联表进行独立性检验，经计算K2=8.01，附表如下：
P（K2≥k0） | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
参照附表，得到的正确的结论是（ ）
A. 有99%以上的把握认为“喜欢乡村音乐与性别有关”
B. 有99%以上的把握认为“喜欢乡村音乐与性别无关”
C. 在犯错误的概率不超过0.1%的前提下，认为“喜欢乡村音乐与性别有关”
D. 在犯错误的概率不超过0.1%的前提下，认为“喜欢乡村音乐与性别无关”