题目内容
已知命题p:方程4x2+4(m-2)x+1=0无实数根;命题q:|m-3|>1.若“p或q”为真命题,“p且q”为假命题,求m的取值范围.
由命题p为真,则△=16(m-2)2-4•4•1<0⇒1<m<3,
由命题q为真,则|m-3|>1⇒m-3<-1或m-3>1⇒m<2或m>4,
由复合命题真值表知,若“p或q”为真命题,“p且q”为假命题,则p,q一真一假,
当p真q假时,则2≤m<3;
当q真p假时,则m≤1或m>4,
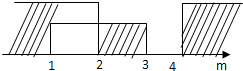
综上m的取值范围m≤1或2≤m<3或m>4.
由命题q为真,则|m-3|>1⇒m-3<-1或m-3>1⇒m<2或m>4,
由复合命题真值表知,若“p或q”为真命题,“p且q”为假命题,则p,q一真一假,
当p真q假时,则2≤m<3;
当q真p假时,则m≤1或m>4,

综上m的取值范围m≤1或2≤m<3或m>4.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
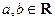 ,若
,若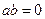 ,则
,则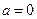 或
或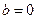 ”
”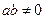 ,则
,则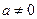 且
且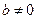 ”;
”;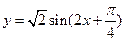 的图象上所有点的横坐标伸长为原来的2倍(纵坐标不变),再向右平移
的图象上所有点的横坐标伸长为原来的2倍(纵坐标不变),再向右平移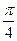 个单位长度,得到函数
个单位长度,得到函数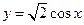 的图象;
的图象;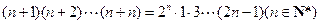 时,从“
时,从“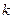 ”到“
”到“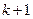 ”的证明,左边需增添的一个因式是
”的证明,左边需增添的一个因式是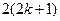 ;
; 有两个零点.
有两个零点.