题目内容
已知命题p：?x∈R，?m∈R，使关于x的方程4x-2x+1+m=0有实数解．如果￢p是真命题，则实数m的取值范围是（ ）
| A．（-∞，1） | B．（-∞，1] | C．[1，+∞） | D．（1，+∞） |
4x-2x+1+m=0得m=4x-2x+1 =（2x）2-2×2x=（2x-1）2+1，
由于2x ＞0，故（2x-1）2+1≥1，∴m≥1，
即命题p为真时，m≥1；命题p为假时，m＜1．
由题意￢p是真命题，则p是假命题，
则实数m的取值范围是（-∞，1）．
故选A．
由于2x ＞0，故（2x-1）2+1≥1，∴m≥1，
即命题p为真时，m≥1；命题p为假时，m＜1．
由题意￢p是真命题，则p是假命题，
则实数m的取值范围是（-∞，1）．
故选A．
练习册系列答案
相关题目
的周期为
②已知数列
的前n项和为Sn，若a1=1且an+1=Sn+1，则数列
的图象关于点（-1，1）对称；④已知命题
：对任意的
，都有
，则
：存在
。其中所有真命题的序号是 。
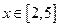或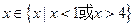
”是假命题，则
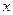的范围是___________。