题目内容
【题目】过直线2x+y+4=0和圆x2+y2+2x﹣4y+1=0的交点,且面积最小的圆方程为( )
A.(x+![]() )2+(y+
)2+(y+![]() )2=
)2=![]() B.(x﹣
B.(x﹣![]() )2+(y﹣
)2+(y﹣![]() )2=
)2=![]()
C.(x﹣![]() )2+(y+
)2+(y+![]() )2=
)2=![]() D.(x+
D.(x+![]() )2+(y﹣
)2+(y﹣![]() )2=
)2=![]()
【答案】D
【解析】
过直线与圆两交点面积最小的圆是以相交弦为直径的圆,由垂径定理求出相交弦长,以及相交弦的中点坐标,即可求解.
圆x2+y2+2x﹣4y+1=0即 (x+1)2+(y﹣2)2=4,
表示以C(﹣1,2)为圆心,半径等于2的圆.
圆心![]() 到直线2x+y+4=0的距离为d=
到直线2x+y+4=0的距离为d=![]() ,
,
故弦长为2![]() =2
=2![]() ,
,
故当面积最小的圆的半径为![]() .
.
过点C且与2x+y+4=0垂直的直线为![]() ,
,
由![]() 求得
求得 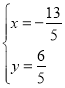 ,
,
即所求圆的圆心为(﹣![]() ,
,![]() ),
),
故所求的圆方程为:(x+![]() )2+(y﹣
)2+(y﹣![]() )2=
)2=![]() .
.
故选:D.

练习册系列答案
相关题目
【题目】某研究机构随机调查了![]() ,
,![]() 两个企业各100名员工,得到了
两个企业各100名员工,得到了![]() 企业员工月均收入的频数分布表以及
企业员工月均收入的频数分布表以及![]() 企业员工月均收入的统计图如下:
企业员工月均收入的统计图如下:
![]() 企业:
企业:
工资 | 人数 |
| 5 |
| 10 |
| 20 |
| 42 |
| 18 |
| 3 |
| 1 |
| 1 |
![]() 企业:
企业:
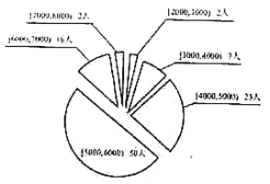
(1)若将频率视为概率,现从![]() 企业中随机抽取一名员工,求该员工月均收入不低于5000元的概率;
企业中随机抽取一名员工,求该员工月均收入不低于5000元的概率;
(2)(i)若从![]() 企业的月均收入在
企业的月均收入在![]() 员工中,按分层抽样的方式抽取7人,而后在此7人中随机抽取2人,则2人月均收入都不在
员工中,按分层抽样的方式抽取7人,而后在此7人中随机抽取2人,则2人月均收入都不在![]() 的概率是多少?
的概率是多少?
(ii)若你是一名即将就业的大学生,根据上述调查结果,并结合统计学相关知识,你会选择去哪个企业就业,并说明理由.