题目内容
15.分别求满足下列条件的直线方程.(1)过点A(2,-1)且与直线y=3x-1垂直;
(2)倾斜角为60°且在y轴上的截距为-3.
分析 (1)由垂直关系可得所求直线的斜率k=-$\frac{1}{3}$,可得点斜式方程,化为一般式可得;
(2)由题意可得得所求的直线的斜率和截距,可得斜截式方程,化为一般式可得.
解答 解:(1)∵已知直线y=3x-1的斜率为3,
∴所求直线的斜率k=-$\frac{1}{3}$
∴所求的直线方程为y+1=-$\frac{1}{3}$(x-2),
化为一般式可得x+3y+1=0;
(2)由题意可得所求的直线的斜率k=tan 60°=$\sqrt{3}$,
又∵直线在y轴上的截距为-3,
∴直线的斜截式方程为y=$\sqrt{3}$x-3,
化为一般式可得$\sqrt{3}$x-y-3=0
点评 本题考查直线的一般式方程和垂直关系,属基础题.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
3.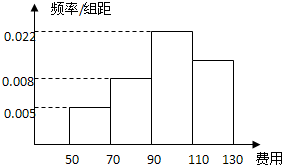 学校为了解学生每周在校费用情况,抽取了n个同学进行调查,结果显示这些同学的支出都在[50,130](单位:元),其中支出在[50,70)(单位:元)的同学有40人,其频率分布直方图如图所示,则支出在[110,130](单位:元)的同学人数是( )
学校为了解学生每周在校费用情况,抽取了n个同学进行调查,结果显示这些同学的支出都在[50,130](单位:元),其中支出在[50,70)(单位:元)的同学有40人,其频率分布直方图如图所示,则支出在[110,130](单位:元)的同学人数是( )
 学校为了解学生每周在校费用情况,抽取了n个同学进行调查,结果显示这些同学的支出都在[50,130](单位:元),其中支出在[50,70)(单位:元)的同学有40人,其频率分布直方图如图所示,则支出在[110,130](单位:元)的同学人数是( )
学校为了解学生每周在校费用情况,抽取了n个同学进行调查,结果显示这些同学的支出都在[50,130](单位:元),其中支出在[50,70)(单位:元)的同学有40人,其频率分布直方图如图所示,则支出在[110,130](单位:元)的同学人数是( )| A. | 100 | B. | 120 | C. | 30 | D. | 300 |
7.若等差数列{an}前n项和Sn=n2+λ,则λ=( )
| A. | 1 | B. | -1 | C. | 0 | D. | 任意实数 |
5.在极坐标系中,已知两点A(2,$\frac{π}{6}$),B(2,-$\frac{π}{6}$),则|AB|=( )
| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | 4 |