题目内容
(本小题满分14分)已知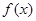 是定义在[-1,1]上的奇函数,当
是定义在[-1,1]上的奇函数,当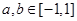 ,且
,且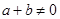 时有
时有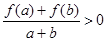 .
.
(1)判断函数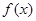 的单调性,并给予证明;
的单调性,并给予证明;
(2)若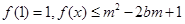 对所有
对所有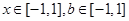 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
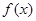 是定义在[-1,1]上的奇函数,当
是定义在[-1,1]上的奇函数,当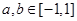 ,且
,且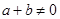 时有
时有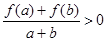 .
.(1)判断函数
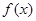 的单调性,并给予证明;
的单调性,并给予证明;(2)若
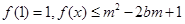 对所有
对所有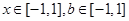 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围. (1)令-1≤x1<x2≤1,且a= x1,b=-x2
则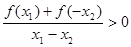 ∵x1- x2<0,f(x)是奇函数
∵x1- x2<0,f(x)是奇函数
∴f(x1)-f(x2)<0即f(x1)<f(x2)
∵x1<x2 ∴f(x)是[-1,1]上的增函数。
(2)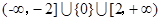 。
。
则
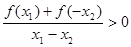 ∵x1- x2<0,f(x)是奇函数
∵x1- x2<0,f(x)是奇函数 ∴f(x1)-f(x2)<0即f(x1)<f(x2)
∵x1<x2 ∴f(x)是[-1,1]上的增函数。
(2)
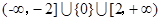 。
。试题分析:(1)
……………6
(2)解:∵f(x)是增函数,且f (x)≤m2-2bm+1对所有x∈[-1,1]恒成立
∴[f(x)]max≤m2-2bm+1 [f(x)]max=f(1)=1
∴m2-2bm+1≥1即m2-2bm≥0在b∈[-1,1]恒成立
∴y= -2mb+m2在b∈[-1,1]恒大于等于0 ……………9
∴
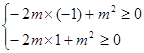 ,∴
,∴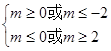
∴m的取值范围是
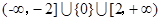 …14
…14点评:对于恒成立问题常用分离参数法进行解决:若
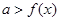 恒成立,只需
恒成立,只需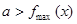 ;若
;若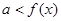 恒成立,只需
恒成立,只需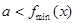 。
。
练习册系列答案
相关题目
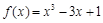 在闭区间 [-3,0] 上的最大值、最小值分别是( )
在闭区间 [-3,0] 上的最大值、最小值分别是( )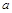 ,计划每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐到面积的一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的
,计划每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐到面积的一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的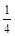 ,已知到今年为止,森林剩余面积为原来的
,已知到今年为止,森林剩余面积为原来的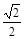 .
.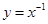 ,
,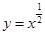 ,
,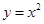 ,
,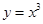 ,,
,,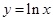 ,
,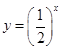 中,在区间
中,在区间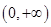 上为减函数的是_________.
上为减函数的是_________.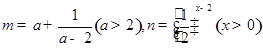 ,则
,则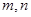 之间的大小关系是
之间的大小关系是 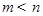
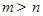
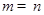
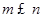
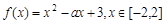 。
。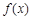 在
在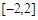 上的最小值是
上的最小值是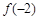 ,试解不等式
,试解不等式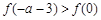 ;
;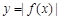 在
在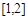 上单调递增,试求实数
上单调递增,试求实数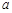 的取值范围。
的取值范围。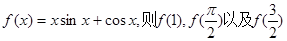 的大小关系是( )
的大小关系是( )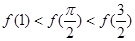
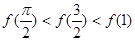
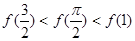
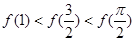
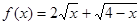 ,则函数
,则函数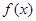 的值域为 ( )
的值域为 ( )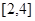


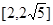
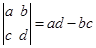
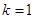 ,解关于
,解关于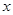 的不等式
的不等式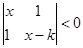
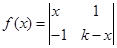 ,对任意
,对任意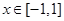 ,都有
,都有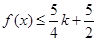 ,求实数
,求实数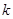 的取值范围。
的取值范围。