题目内容
5.已知等差数列{an},又a1,a2,a5成等比数列且a2,a3+2,a6成等差数列(Ⅰ)求数列{an}的通项an;
(Ⅱ)定义:$\frac{n}{{{P_1}+{P_2}+…+{P_n}}}$为n个正数P1,P2,P3,…,Pn( n∈N*)的“均倒数”,
(ⅰ)若数列{bn}前n项的“均倒数”为$\frac{1}{a_n}$(n∈N*),求数列{bn}的通项bn;
(ⅱ)求$\frac{1}{{{b_1}•{b_2}}}+\frac{1}{{{b_2}•{b_3}}}+…+\frac{1}{{{b_n}•{b_{n+1}}}}$.
分析 (Ⅰ)通过a2,a3+2,a6成等差数列,计算即得结论;
(Ⅱ)(ⅰ)通过计算可得$\frac{n}{{{b_1}+{b_2}+…+{b_n}}}=\frac{1}{2n-1}$,利用b1+b2+…bn与b1+b2+…bn-1的差计算即得结论;(ⅱ)通过对$\frac{1}{{b}_{n}{b}_{n+1}}$分离分母,并项相加即得结论.
解答 解:(Ⅰ)设数列{an}的公差为d,
由題意有:$\left\{\begin{array}{l}{({a_1}+d)^2}={a_1}({a_1}+4d)\\ 2({a_1}+2d+2)=2{a_1}+6d\end{array}\right.$,
解得$\left\{\begin{array}{l}{a_1}=1\\ d=2\end{array}\right.$,∴an=2n-1;
(Ⅱ)(ⅰ)由题意有:$\frac{n}{{{b_1}+{b_2}+…+{b_n}}}=\frac{1}{2n-1}$,
∴b1+b2+…bn=n•(2n-1),①
b1+b2+…bn-1=(n-1)•[2(n-1)-1](n≥2)②
由①-②得:bn=4n-3(n≥2),
又b1=1,∴bn=4n-3(n∈N*);
(ⅱ)∵$\frac{1}{{{b_n}{b_{n+1}}}}=\frac{1}{(4n-3)•(4n+1)}=\frac{1}{4}[\frac{1}{4n-3}-\frac{1}{4n+1}]$,
∴$\frac{1}{{{b_1}•{b_2}}}+\frac{1}{{{b_2}•{b_3}}}+…+\frac{1}{{{b_n}•{b_{n+1}}}}$
=$\frac{1}{4}[{({1-\frac{1}{5}})+({\frac{1}{5}-\frac{1}{9}})+…+({\frac{1}{4n-3}-\frac{1}{4n+1}})}]$
=$\frac{1}{4}({1-\frac{1}{4n+1}})=\frac{n}{4n+1}$.
点评 本题考查求数列的通项,考查运算求解能力,注意解题方法的积累,属于中档题.

| A. | 由样本数据得到的回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$必过样本中心($\overline{x}$,$\overline{y}$) | |
| B. | 残差平方和越小的模型,拟合的效果越好 | |
| C. | 用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好 | |
| D. | 两个随机变量的线性相关性越强,相关系数的绝对值越接近于1 |
| A. | $\sqrt{3}$倍 | B. | 2倍 | C. | $\sqrt{2}$倍 | D. | $\frac{3}{2}$倍 |
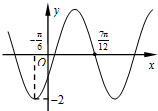 已知函数f(x)=2sin(ωx+θ ) (ω>0)的图象如图所示,则ω=2,若将函数f(x)的图象向左平移φ $({0<φ<\frac{π}{2}})$个单位后得到一个偶函数,则φ=$\frac{π}{3}$.
已知函数f(x)=2sin(ωx+θ ) (ω>0)的图象如图所示,则ω=2,若将函数f(x)的图象向左平移φ $({0<φ<\frac{π}{2}})$个单位后得到一个偶函数,则φ=$\frac{π}{3}$.