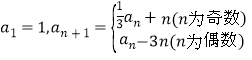题目内容
【题目】已知指数函数![]() 的图象经过点
的图象经过点![]() ,
,![]() 在区间
在区间![]() 的最小值
的最小值![]() ;
;
(1)求函数![]() 的解析式;
的解析式;
(2)求函数![]() 的最小值
的最小值![]() 的表达式;
的表达式;
(3)是否存在![]() 同时满足以下条件:①
同时满足以下条件:①![]() ;②当
;②当![]() 的定义域为
的定义域为![]() 时,值域为
时,值域为![]() ;若存在,求出m,n的值;若不存在,说明理由.
;若存在,求出m,n的值;若不存在,说明理由.
【答案】(1)![]() (2)
(2)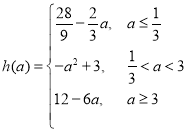 (3)不存在,理由见解析
(3)不存在,理由见解析
【解析】
(1)设![]() ,由点
,由点![]() 在图象上,得出
在图象上,得出![]() ,求出
,求出![]() 的值,即可得出函数
的值,即可得出函数![]() 的解析式;
的解析式;
(2)利用换元法得出![]() ,讨论
,讨论![]() 的取值,由二次函数的性质得出函数
的取值,由二次函数的性质得出函数![]() 的最小值
的最小值![]() 的表达式;
的表达式;
(3)当![]() 时,函数
时,函数![]() 在
在![]() 上为减函数,由值域为
上为减函数,由值域为![]() ,列出方程组,得出
,列出方程组,得出![]() ,由于
,由于![]() ,则不存在满足条件的
,则不存在满足条件的![]() 的值.
的值.
(1)设![]() ,
,![]() 且
且![]()
∵指数函数![]() 的图象经过点
的图象经过点![]() ,∴
,∴![]() ,即
,即![]() ,∴
,∴![]() ,
,
(2)令![]() ,∵
,∵![]()
∴![]()
∴![]() ,对称轴为
,对称轴为![]()
当![]() 时,
时,![]() 在
在![]() 上为增函数,此时当
上为增函数,此时当![]() 时,
时,![]()
当![]() 时,
时,![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数,此时当
上为增函数,此时当![]() 时,
时,![]()
当![]() 时,
时,![]() 在
在![]() 上为减函数,此时当
上为减函数,此时当![]() 时,
时,![]()
∴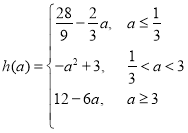 .
.
(3)由(2)得![]() 时,
时,![]() 在
在![]() 中为减函数,若此时
中为减函数,若此时![]() 值域为
值域为![]() .则
.则 ,即
,即![]() ,即
,即![]() ,与
,与![]() 矛盾,故不存在满足条件的
矛盾,故不存在满足条件的![]() 的值.
的值.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
【题目】某工厂的![]() ,
,![]() ,
,![]() 三个不同车间生产同一产品的数量(单位:件)如下表所示.质检人员用分层抽样的方法从这些产品中共抽取6件样品进行检测:
三个不同车间生产同一产品的数量(单位:件)如下表所示.质检人员用分层抽样的方法从这些产品中共抽取6件样品进行检测:
车间 |
|
|
|
数量 | 50 | 150 | 100 |
(1)求这6件样品中来自![]() ,
,![]() ,
,![]() 各车间产品的数量;
各车间产品的数量;
(2)若在这6件样品中随机抽取2件进行进一步检测,求这2件产品来自相同车间的概率.