题目内容
【题目】如图,在三棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
(1)证明:![]() 平面
平面![]() ;
;
(2)若点![]() 在棱
在棱![]() 上,且
上,且![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.

【答案】解:
(1)因为AP=CP=AC=4,O为AC的中点,所以OP⊥AC,且OP=![]() .
.
连结OB.因为AB=BC=![]() ,所以△ABC为等腰直角三角形,且OB⊥AC,OB=
,所以△ABC为等腰直角三角形,且OB⊥AC,OB=![]() =2.
=2.
由![]() 知,OP⊥OB.
知,OP⊥OB.
由OP⊥OB,OP⊥AC知PO⊥平面ABC.
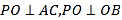
(2)作CH⊥OM,垂足为H.又由(1)可得OP⊥CH,所以CH⊥平面POM.
故CH的长为点C到平面POM的距离.
由题设可知OC=![]() =2,CM=
=2,CM=![]() =
=![]() ,∠ACB=45°.
,∠ACB=45°.
所以OM=![]() ,CH=
,CH=![]() =
=![]() .
.
所以点C到平面POM的距离为![]() .
.
【解析】分析:(1)连接![]() ,欲证
,欲证![]() 平面
平面![]() ,只需证明
,只需证明![]() 即可;(2)过点
即可;(2)过点![]() 作
作![]() ,垂足为
,垂足为![]() ,只需论证
,只需论证![]() 的长即为所求,再利用平面几何知识求解即可.
的长即为所求,再利用平面几何知识求解即可.
详解:(1)因为AP=CP=AC=4,O为AC的中点,所以OP⊥AC,且OP=![]() .
.
连结OB.因为AB=BC=![]() ,所以△ABC为等腰直角三角形,且OB⊥AC,OB=
,所以△ABC为等腰直角三角形,且OB⊥AC,OB=![]() =2.
=2.
由![]() 知,OP⊥OB.
知,OP⊥OB.
由OP⊥OB,OP⊥AC知PO⊥平面ABC.
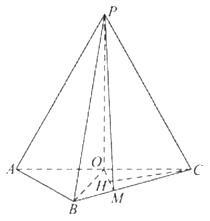
(2)作CH⊥OM,垂足为H.又由(1)可得OP⊥CH,所以CH⊥平面POM.
故CH的长为点C到平面POM的距离.
由题设可知OC=![]() =2,CM=
=2,CM=![]() =
=![]() ,∠ACB=45°.
,∠ACB=45°.
所以OM=![]() ,CH=
,CH=![]() =
=![]() .
.
所以点C到平面POM的距离为![]() .
.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目