题目内容
【题目】已知函数![]() 是定义域为
是定义域为![]() 上的奇函数,且
上的奇函数,且![]() .
.
(1)用定义证明:函数![]() 在
在![]() 上是增函数;
上是增函数;
(2)若实数t满足![]() 求实数t的范围.
求实数t的范围.
【答案】(1)见解析(2)(0,![]() )
)
【解析】
(1)由函数![]() 是定义域为(﹣1,1)上的奇函数,求出b=0,从而
是定义域为(﹣1,1)上的奇函数,求出b=0,从而![]() ,利用定义法能证明函数f(x)在(﹣1,1)上是增函数;
,利用定义法能证明函数f(x)在(﹣1,1)上是增函数;
(2)推导出f(2t﹣1)<f(1﹣t),由函数f(x)在(﹣1,1)上是增函数,列出不等式组,由此能求出实数t的范围.
解:(1)∵函数![]() 是定义域为(﹣1,1)上的奇函数,
是定义域为(﹣1,1)上的奇函数,
∴f(0)![]() 0,∴b=0,
0,∴b=0,
∴![]()
任取x1,x2∈(﹣1,1),且x1<x2,
∴f(x1)﹣f(x2)![]()
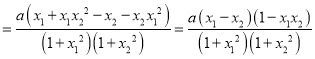 ,
,
∵a>0,﹣1<x1<x2<1,
∴x1﹣x2<0,1﹣x1x2>0,1![]() 0,1
0,1![]() 0,
0,
∴函数f(x)在(﹣1,1)上是增函数.
(2)∵f(2t﹣1)+f(t﹣1)<0,∴f(2t﹣1)<﹣f(t﹣1),
∵函数![]() 是定义域为(﹣1,1)上的奇函数,且a>0.
是定义域为(﹣1,1)上的奇函数,且a>0.
∴f(2t﹣1)<f(1﹣t),
∵函数f(x)在(﹣1,1)上是增函数,
∴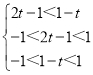 ,
,
解得0<t![]() .
.
故实数t的范围是(0,![]() ).
).

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
【题目】某互联网公司为了确定下一季度的前期广告投入计划,收集了近![]() 个月广告投入量
个月广告投入量![]() (单位:万元)和收益
(单位:万元)和收益![]() (单位:万元)的数据如下表:
(单位:万元)的数据如下表:
月份 |
|
|
|
|
|
|
广告投入量 |
|
|
|
|
|
|
收益 |
|
|
|
|
|
|
他们分别用两种模型①![]() ,②
,②![]() 分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值:
分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值:
|
|
|
|
|
|
|
|

(Ⅰ)根据残差图,比较模型①,②的拟合效果,应选择哪个模型?并说明理由;
(Ⅱ)残差绝对值大于![]() 的数据被认为是异常数据,需要剔除:
的数据被认为是异常数据,需要剔除:
(ⅰ)剔除异常数据后求出(Ⅰ)中所选模型的回归方程
(ⅱ)若广告投入量![]() 时,该模型收益的预报值是多少?
时,该模型收益的预报值是多少?
附:对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
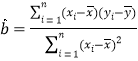
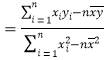 ,
,![]() .
.