题目内容
【题目】已知二次函数![]() 满足
满足![]()
(1)求函数![]() 的解析式;
的解析式;
(2)令![]()
若函数在![]() 上是单调函数,求实数m的取值范围;
上是单调函数,求实数m的取值范围;
求函数![]() 在
在![]() 的最小值.
的最小值.
【答案】(1)f(x)=﹣x2+2x+15(2)①m≤0,或m≥2②见解析
【解析】
(1)据二次函数的形式设出f(x)的解析式,将已知条件代入,列出方程,令方程两边的对应系数相等解得.
(2)函数g(x)的图象是开口朝上,且以x=m为对称轴的抛物线,
①若函数g(x)在x∈[0,2]上是单调函数,则m≤0,或m≥2;
②分当m≤0时,当0<m<2时,当m≥2时三种情况分别求出函数的最小值,可得答案.
解:(1)设f(x)=ax2+bx+c,
∵f(2)=15,f(x+1)﹣f(x)=﹣2x+1,
∴4a+2b+c=15;a(x+1)2+b(x+1)+c﹣(ax2+bx+c)=﹣2x+1;
∴2a=﹣2,a+b=1,4a+2b+c=15,解得a=﹣1,b=2,c=15,
∴函数f(x)的表达式为f(x)=﹣x2+2x+15;
(2)∵g(x)=(2﹣2m)x﹣f(x)=x2﹣2mx﹣15的图象是开口朝上,且以x=m为对称轴的抛物线,
①若函数g(x)在x∈[0,2]上是单调函数,则m≤0,或m≥2;
②当m≤0时,g(x)在[0,2]上为增函数,当x=0时,函数g(x)取最小值﹣15;
当0<m<2时,g(x)在[0,m]上为减函数,在[m,2]上为增函数,当x=m时,函数g(x)取最小值﹣m2﹣15;
当m≥2时,g(x)在[0,2]上为减函数,当x=2时,函数g(x)取最小值﹣4m﹣11;
∴函数g(x)在x∈[0,2]的最小值为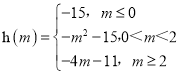

 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案【题目】某种商品价格与该商品日需求量之间的几组对照数据如下表,经过进一步统计分析,发现y与x具有线性相关关系.
价格x(元/kg) | 10 | 15 | 20 | 25 | 30 |
日需求量y(kg) | 11 | 10 | 8 | 6 | 5 |
(1)根据上表给出的数据,求出y与x的线性回归方程![]() ;
;
(2)利用(1)中的回归方程,当价格![]() 元/kg时,日需求量y的预测值为多少?
元/kg时,日需求量y的预测值为多少?
(参考公式:线性回归方程![]() ,其中
,其中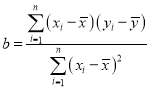 ,
,![]() .)
.)