题目内容
4.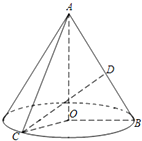 如图,在Rt△AOB中,∠OAB=$\frac{π}{6}$,斜边AB=4,D是AB的中点.现将Rt△AOB以直角边AO为轴旋转一周得到一个圆锥,点C为圆锥底面圆周上的一点,且∠BOC=$\frac{π}{2}$.
如图,在Rt△AOB中,∠OAB=$\frac{π}{6}$,斜边AB=4,D是AB的中点.现将Rt△AOB以直角边AO为轴旋转一周得到一个圆锥,点C为圆锥底面圆周上的一点,且∠BOC=$\frac{π}{2}$.(1)求该圆锥的全面积;
(2)求异面直线AO与CD所成角的大小.
(结果用反三角函数值表示)
分析 (1)求出圆锥底面半径,圆锥的侧面积S侧,然后求解圆锥的全面积.
(2)过D作DM∥AO交BO于M,连CM,说明∠CDM为异面直线AO与CD所成角,在Rt△CDM中,求解异面直线AO与CD所成角的大小.
解答 解:(1)Rt△AOB中,OB=2
即圆锥底面半径为2
圆锥的侧面积S侧=πrl=8π….4’
故圆锥的全面积S全=S侧+S底=8π+4π=12π….6’
(2)过D作DM∥AO交BO于M,连CM
则∠CDM为异面直线AO与CD所成角….8’
∵AO⊥平面OBC∴DM⊥平面OBC∴DM⊥MC
在Rt△AOB中,$AO=2\sqrt{3}$∴$DM=\sqrt{3}$,
∵D是AB的中点∴M是OB的中点,
∴OM=1∴$CM=\sqrt{5}$.
在Rt△CDM中,$tan∠CDM=\frac{{\sqrt{5}}}{{\sqrt{3}}}=\frac{{\sqrt{15}}}{3}$,….10’
∴$∠CDM=arctan\frac{{\sqrt{15}}}{3}$,
即异面直线AO与CD所成角的大小为$arctan\frac{{\sqrt{15}}}{3}$….12’
点评 本题考查异面直线所成角的求法,几何体的全面积的求法,考查空间想象能力以及计算能力.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
14.下表是某同学五次数学附加题测试的得分,则该组数据的方差为$\frac{146}{5}$.
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 分数 | 36 | 21 | 30 | 28 | 35 |
14.已知函数f(x)=$\left\{\begin{array}{l}x+1,\;\;x≤0\\{2^x}-4,\;\;x>0\end{array}$,若函数y=f[f(x)+a]有四个零点,则实数a的取值范围为( )
| A. | [-2,2) | B. | [1,5) | C. | [1,2) | D. | [-2,5) |
 在正方体ABCD-A1B1C1D1中,已知M,N分别是A1B1,BB1的中点,过M,N,C1的截面截正方体所得的几何体,如图所示,那么该几何体的侧视图是( )
在正方体ABCD-A1B1C1D1中,已知M,N分别是A1B1,BB1的中点,过M,N,C1的截面截正方体所得的几何体,如图所示,那么该几何体的侧视图是( )



 如图,在执行程序框图所示的算法时,若输入a3,a2,a1,a0的值依次是1,-3,3,-1,则输出v的值为( )
如图,在执行程序框图所示的算法时,若输入a3,a2,a1,a0的值依次是1,-3,3,-1,则输出v的值为( )